Delta-LoRA: Fine-Tuning High-Rank Parameters with the Delta of Low-Rank Matrices
Paper and Code
Sep 05, 2023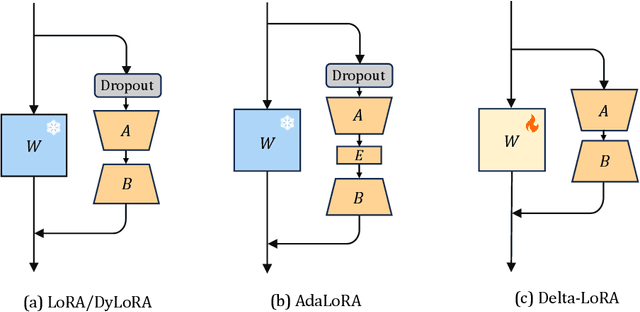
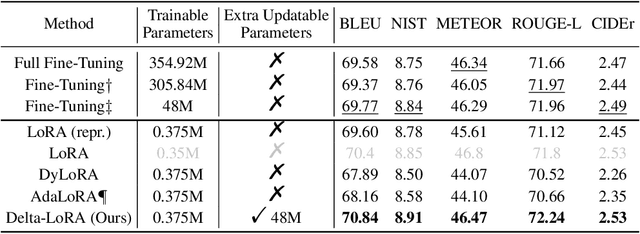
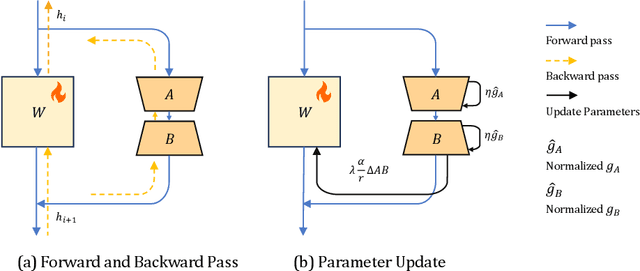
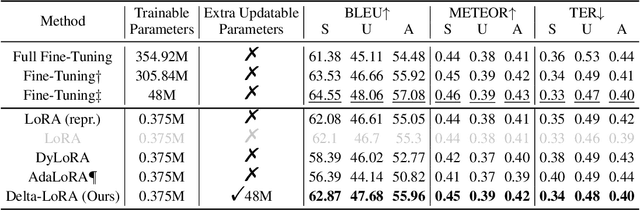
In this paper, we present Delta-LoRA, which is a novel parameter-efficient approach to fine-tune large language models (LLMs). In contrast to LoRA and other low-rank adaptation methods such as AdaLoRA, Delta-LoRA not only updates the low-rank matrices $\bA$ and $\bB$, but also propagate the learning to the pre-trained weights $\bW$ via updates utilizing the delta of the product of two low-rank matrices ($\bA^{(t+1)}\bB^{(t+1)} - \bA^{(t)}\bB^{(t)}$). Such a strategy effectively addresses the limitation that the incremental update of low-rank matrices is inadequate for learning representations capable for downstream tasks. Moreover, as the update of $\bW$ does not need to compute the gradients of $\bW$ and store their momentums, Delta-LoRA shares comparable memory requirements and computational costs with LoRA. Extensive experiments show that Delta-LoRA significantly outperforms existing low-rank adaptation methods. We further support these results with comprehensive analyses that underscore the effectiveness of Delta-LoRA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge