Delay-Tolerant Constrained OCO with Application to Network Resource Allocation
Paper and Code
May 09, 2021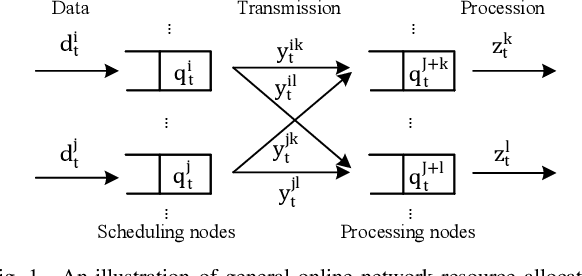
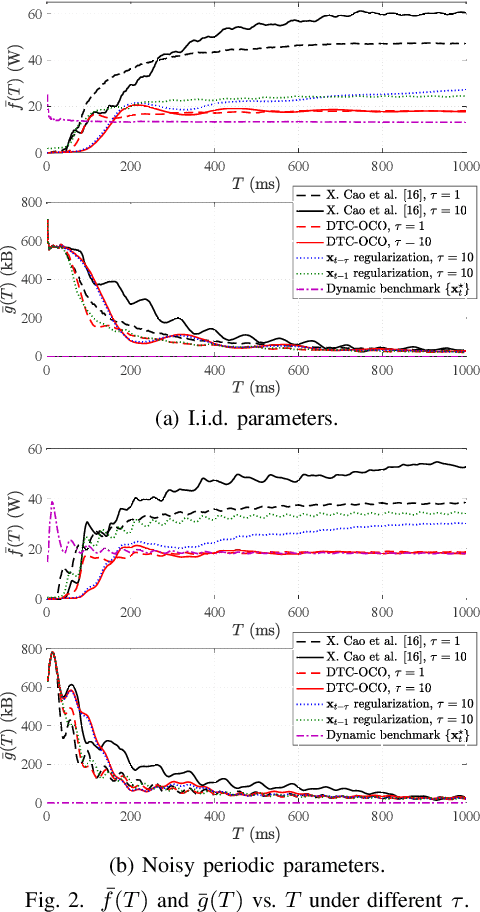

We consider online convex optimization (OCO) with multi-slot feedback delay, where an agent makes a sequence of online decisions to minimize the accumulation of time-varying convex loss functions, subject to short-term and long-term constraints that are possibly time-varying. The current convex loss function and the long-term constraint function are revealed to the agent only after the decision is made, and they may be delayed for multiple time slots. Existing work on OCO under this general setting has focused on the static regret, which measures the gap of losses between the online decision sequence and an offline benchmark that is fixed over time. In this work, we consider both the static regret and the more practically meaningful dynamic regret, where the benchmark is a time-varying sequence of per-slot optimizers. We propose an efficient algorithm, termed Delay-Tolerant Constrained-OCO (DTC-OCO), which uses a novel constraint penalty with double regularization to tackle the asynchrony between information feedback and decision updates. We derive upper bounds on its dynamic regret, static regret, and constraint violation, proving them to be sublinear under mild conditions. We further apply DTC-OCO to a general network resource allocation problem, which arises in many systems such as data networks and cloud computing. Simulation results demonstrate substantial performance gain of DTC-OCO over the known best alternative.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge