DeepPCR: Parallelizing Sequential Operations in Neural Networks

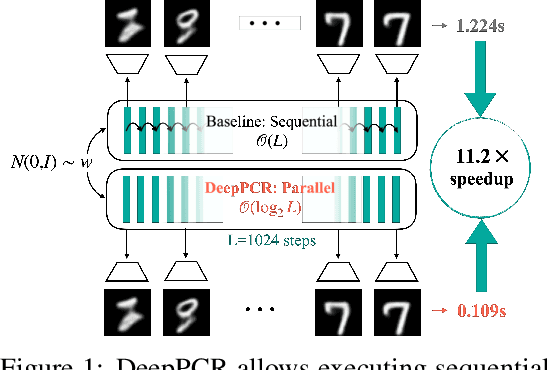
Parallelization techniques have become ubiquitous for accelerating inference and training of deep neural networks. Despite this, several operations are still performed in a sequential manner. For instance, the forward and backward passes are executed layer-by-layer, and the output of diffusion models is produced by applying a sequence of denoising steps. This sequential approach results in a computational cost proportional to the number of steps involved, presenting a potential bottleneck as the number of steps increases. In this work, we introduce DeepPCR, a novel algorithm which parallelizes typically sequential operations used in inference and training of neural networks. DeepPCR is based on interpreting a sequence of $L$ steps as the solution of a specific system of equations, which we recover using the Parallel Cyclic Reduction algorithm. This reduces the complexity of computing the sequential operations from $\mathcal{O}(L)$ to $\mathcal{O}(\log_2L)$, thus yielding a speedup for large $L$. To verify the theoretical lower complexity of the algorithm, and to identify regimes for speedup, we test the effectiveness of DeepPCR in parallelizing the forward and backward pass in multi-layer perceptrons, and reach speedups of up to $30\times$ for forward and $200\times$ for backward pass. We additionally showcase the flexibility of DeepPCR by parallelizing training of ResNets with as many as 1024 layers, and generation in diffusion models, enabling up to $7\times$ faster training and $11\times$ faster generation, respectively, when compared to the sequential approach.