Deep Generative Learning via Variational Gradient Flow
Paper and Code
Feb 07, 2019
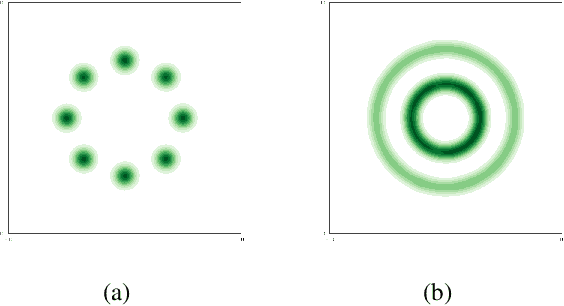
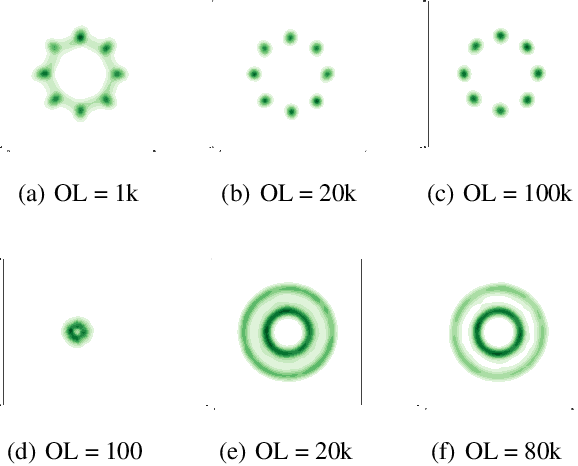
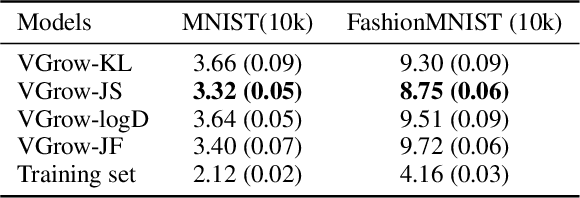
We propose a general framework to learn deep generative models via \textbf{V}ariational \textbf{Gr}adient Fl\textbf{ow} (VGrow) on probability spaces. The evolving distribution that asymptotically converges to the target distribution is governed by a vector field, which is the negative gradient of the first variation of the $f$-divergence between them. We prove that the evolving distribution coincides with the pushforward distribution through the infinitesimal time composition of residual maps that are perturbations of the identity map along the vector field. The vector field depends on the density ratio of the pushforward distribution and the target distribution, which can be consistently learned from a binary classification problem. Connections of our proposed VGrow method with other popular methods, such as VAE, GAN and flow-based methods, have been established in this framework, gaining new insights of deep generative learning. We also evaluated several commonly used divergences, including Kullback-Leibler, Jensen-Shannon, Jeffrey divergences as well as our newly discovered `logD' divergence which serves as the objective function of the logD-trick GAN. Experimental results on benchmark datasets demonstrate that VGrow can generate high-fidelity images in a stable and efficient manner, achieving competitive performance with state-of-the-art GANs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge