Deep Architecture Connectivity Matters for Its Convergence: A Fine-Grained Analysis

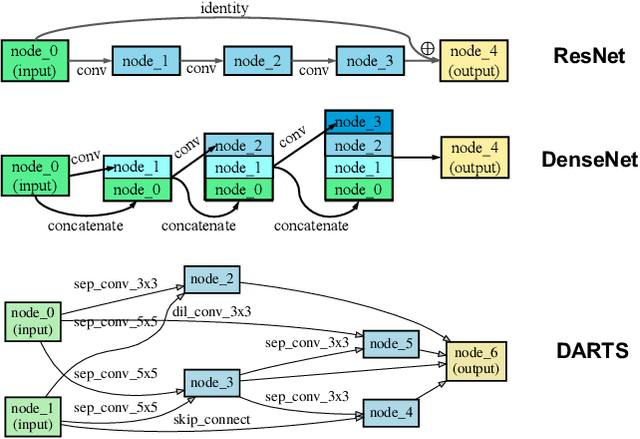
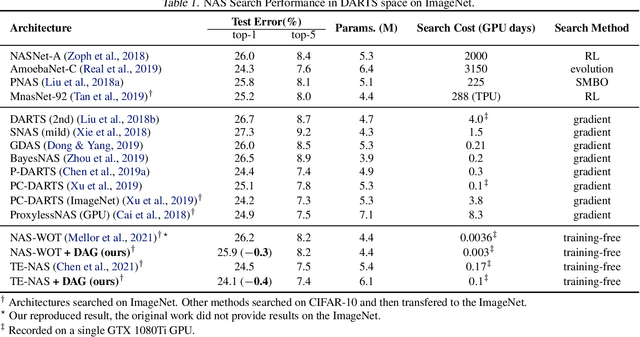
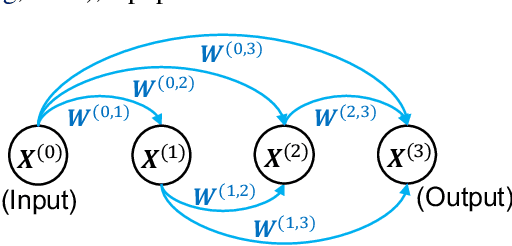
Advanced deep neural networks (DNNs), designed by either human or AutoML algorithms, are growing increasingly complex. Diverse operations are connected by complicated connectivity patterns, e.g., various types of skip connections. Those topological compositions are empirically effective and observed to smooth the loss landscape and facilitate the gradient flow in general. However, it remains elusive to derive any principled understanding of their effects on the DNN capacity or trainability, and to understand why or in which aspect one specific connectivity pattern is better than another. In this work, we theoretically characterize the impact of connectivity patterns on the convergence of DNNs under gradient descent training in fine granularity. By analyzing a wide network's Neural Network Gaussian Process (NNGP), we are able to depict how the spectrum of an NNGP kernel propagates through a particular connectivity pattern, and how that affects the bound of convergence rates. As one practical implication of our results, we show that by a simple filtration on "unpromising" connectivity patterns, we can trim down the number of models to evaluate, and significantly accelerate the large-scale neural architecture search without any overhead. Codes will be released at https://github.com/chenwydj/architecture_convergence.