Customized Monte Carlo Tree Search for LLVM/Polly's Composable Loop Optimization Transformations
Paper and Code
May 10, 2021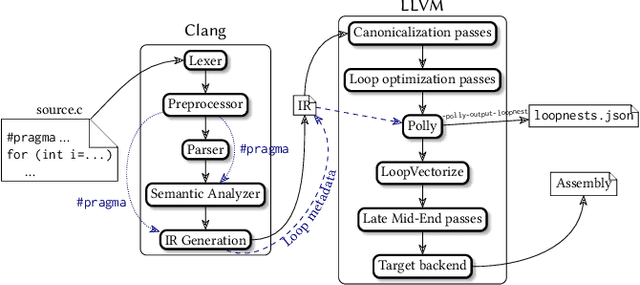
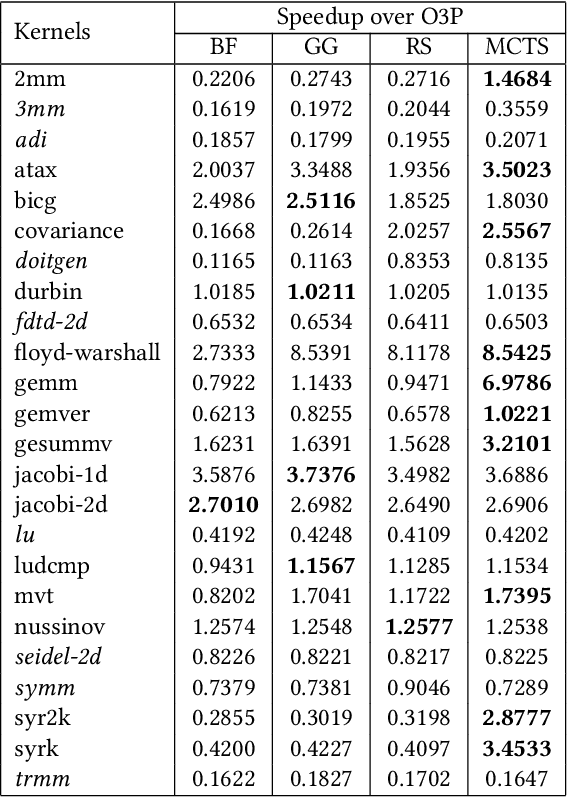
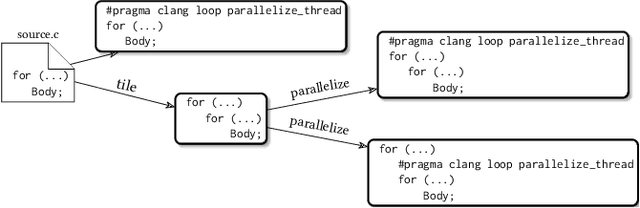
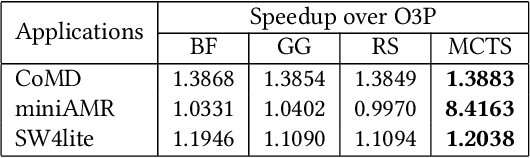
Polly is the LLVM project's polyhedral loop nest optimizer. Recently, user-directed loop transformation pragmas were proposed based on LLVM/Clang and Polly. The search space exposed by the transformation pragmas is a tree, wherein each node represents a specific combination of loop transformations that can be applied to the code resulting from the parent node's loop transformations. We have developed a search algorithm based on Monte Carlo tree search (MCTS) to find the best combination of loop transformations. Our algorithm consists of two phases: exploring loop transformations at different depths of the tree to identify promising regions in the tree search space and exploiting those regions by performing a local search. Moreover, a restart mechanism is used to avoid the MCTS getting trapped in a local solution. The best and worst solutions are transferred from the previous phases of the restarts to leverage the search history. We compare our approach with random, greedy, and breadth-first search methods on PolyBench kernels and ECP proxy applications. Experimental results show that our MCTS algorithm finds pragma combinations with a speedup of 2.3x over Polly's heuristic optimizations on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge