CPDist: Deep Siamese Networks for Learning Distances Between Structured Preferences

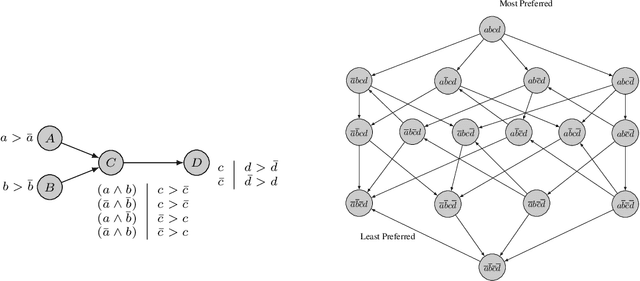
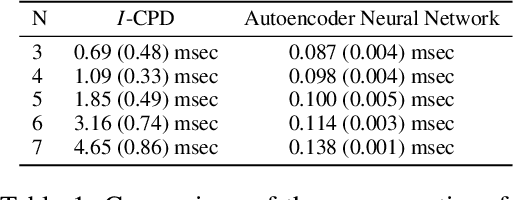
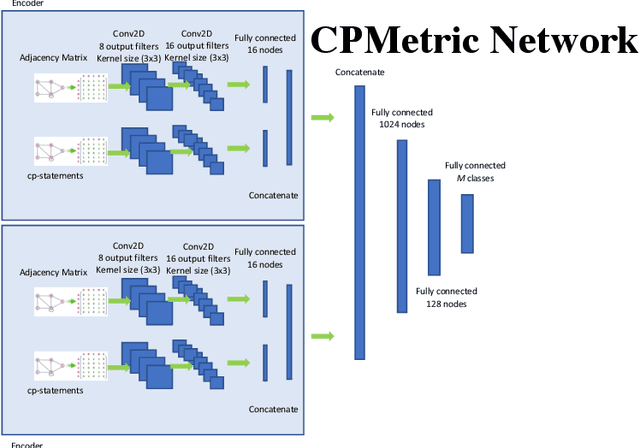
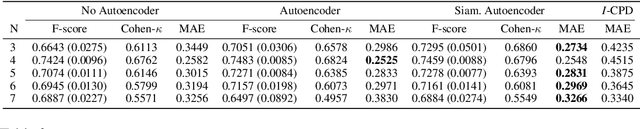
Preference are central to decision making by both machines and humans. Representing, learning, and reasoning with preferences is an important area of study both within computer science and across the sciences. When working with preferences it is necessary to understand and compute the distance between sets of objects, e.g., the preferences of a user and a the descriptions of objects to be recommended. We present CPDist, a novel neural network to address the problem of learning to measure the distance between structured preference representations. We use the popular CP-net formalism to represent preferences and then leverage deep neural networks to learn a recently proposed metric function that is computationally hard to compute directly. CPDist is a novel metric learning approach based on the use of deep siamese networks which learn the Kendal Tau distance between partial orders that are induced by compact preference representations. We find that CPDist is able to learn the distance function with high accuracy and outperform existing approximation algorithms on both the regression and classification task using less computation time. Performance remains good even when CPDist is trained with only a small number of samples compared to the dimension of the solution space, indicating the network generalizes well.