Covariance-Based Activity Detection in Cooperative Multi-Cell Massive MIMO: Scaling Law and Efficient Algorithms
Paper and Code
Nov 26, 2023


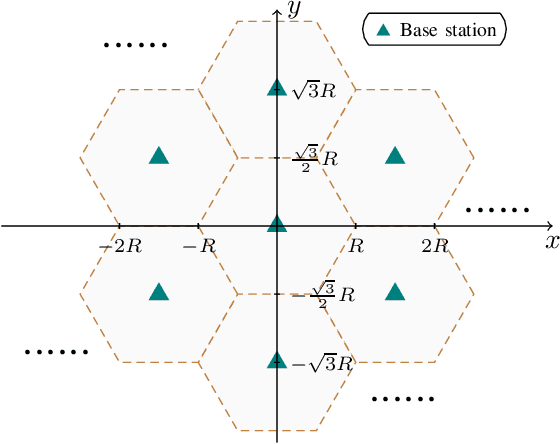
This paper focuses on the covariance-based activity detection problem in a multi-cell massive multiple-input multiple-output (MIMO) system. In this system, active devices transmit their signature sequences to multiple base stations (BSs), and the BSs cooperatively detect the active devices based on the received signals. While the scaling law for the covariance-based activity detection in the single-cell scenario has been extensively analyzed in the literature, this paper aims to analyze the scaling law for the covariance-based activity detection in the multi-cell massive MIMO system. Specifically, this paper demonstrates a quadratic scaling law in the multi-cell system, under the assumption that the exponent in the classical path-loss model is greater than 2. This finding shows that, in the multi-cell MIMO system, the maximum number of active devices that can be detected correctly in each cell increases quadratically with the length of the signature sequence and decreases logarithmically with the number of cells (as the number of antennas tends to infinity). Moreover, in addition to analyzing the scaling law for the signature sequences randomly and uniformly distributed on a sphere, the paper also establishes the scaling law for signature sequences generated from a finite alphabet, which are easier to generate and store. Moreover, this paper proposes two efficient accelerated coordinate descent (CD) algorithms with a convergence guarantee for solving the device activity detection problem. The first algorithm reduces the complexity of CD by using an inexact coordinate update strategy. The second algorithm avoids unnecessary computations of CD by using an active set selection strategy. Simulation results show that the proposed algorithms exhibit excellent performance in terms of computational efficiency and detection error probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge