CoT: Cooperative Training for Generative Modeling of Discrete Data

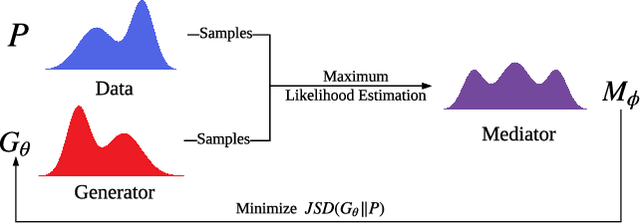
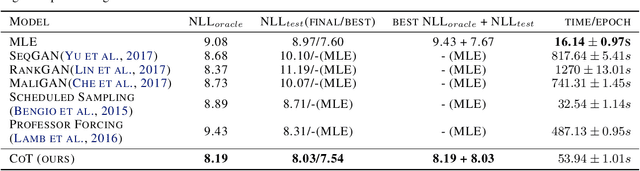
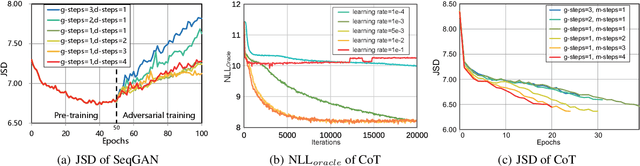
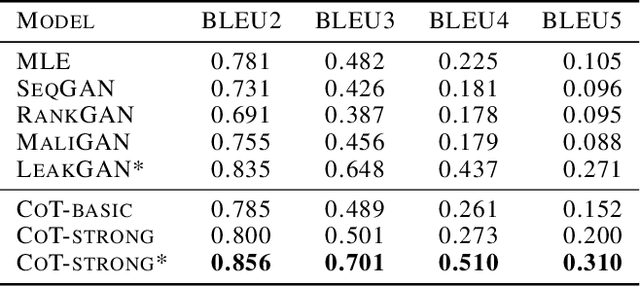
We propose Cooperative Training (CoT) for training generative models that measure a tractable density for discrete data. CoT coordinately trains a generator $G$ and an auxiliary predictive mediator $M$. The training target of $M$ is to estimate a mixture density of the learned distribution $G$ and the target distribution $P$, and that of $G$ is to minimize the Jensen-Shannon divergence estimated through $M$. CoT achieves independent success without the necessity of pre-training via Maximum Likelihood Estimation or involving high-variance algorithms like REINFORCE. This low-variance algorithm is theoretically proved to be unbiased for both generative and predictive tasks. We also theoretically and empirically show the superiority of CoT over most previous algorithms in terms of generative quality and diversity, predictive generalization ability and computational cost.