Convolutional Normalizing Flows for Deep Gaussian Processes
Paper and Code
Apr 23, 2021
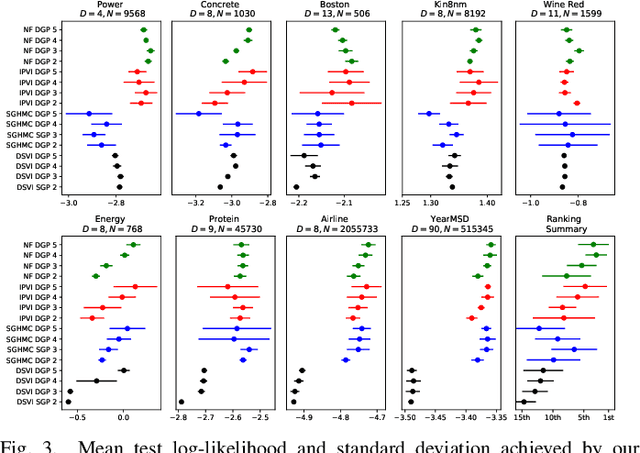
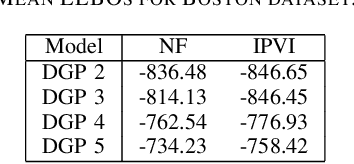
Deep Gaussian processes (DGPs), a hierarchical composition of GP models, have successfully boosted the expressive power of their single-layer counterpart. However, it is impossible to perform exact inference in DGPs, which has motivated the recent development of variational inference-based methods. Unfortunately, either these methods yield a biased posterior belief or it is difficult to evaluate their convergence. This paper introduces a new approach for specifying flexible, arbitrarily complex, and scalable approximate posterior distributions. The posterior distribution is constructed through a normalizing flow (NF) which transforms a simple initial probability into a more complex one through a sequence of invertible transformations. Moreover, a novel convolutional normalizing flow (CNF) is developed to improve the time efficiency and capture dependency between layers. Empirical evaluation shows that CNF DGP outperforms the state-of-the-art approximation methods for DGPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge