Convergence Rates of Average-Reward Multi-agent Reinforcement Learning via Randomized Linear Programming
Paper and Code
Oct 22, 2021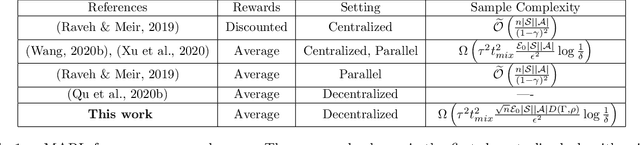
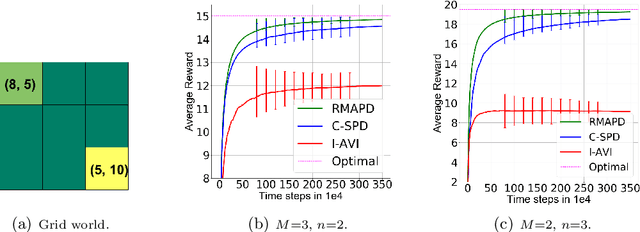
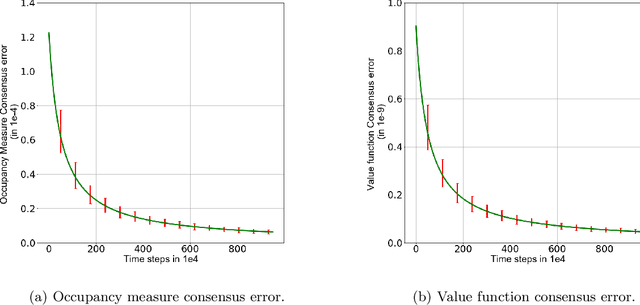
In tabular multi-agent reinforcement learning with average-cost criterion, a team of agents sequentially interacts with the environment and observes local incentives. We focus on the case that the global reward is a sum of local rewards, the joint policy factorizes into agents' marginals, and full state observability. To date, few global optimality guarantees exist even for this simple setting, as most results yield convergence to stationarity for parameterized policies in large/possibly continuous spaces. To solidify the foundations of MARL, we build upon linear programming (LP) reformulations, for which stochastic primal-dual methods yields a model-free approach to achieve \emph{optimal sample complexity} in the centralized case. We develop multi-agent extensions, whereby agents solve their local saddle point problems and then perform local weighted averaging. We establish that the sample complexity to obtain near-globally optimal solutions matches tight dependencies on the cardinality of the state and action spaces, and exhibits classical scalings with respect to the network in accordance with multi-agent optimization. Experiments corroborate these results in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge