Convergence and Consistency Analysis for A 3D Invariant-EKF SLAM
Paper and Code
Feb 22, 2017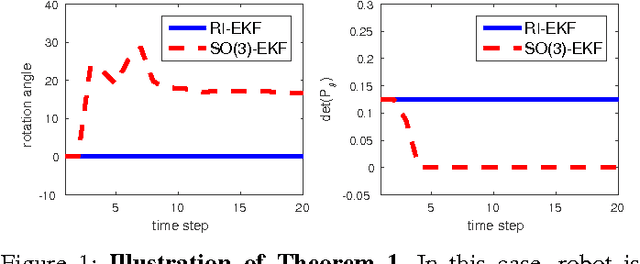
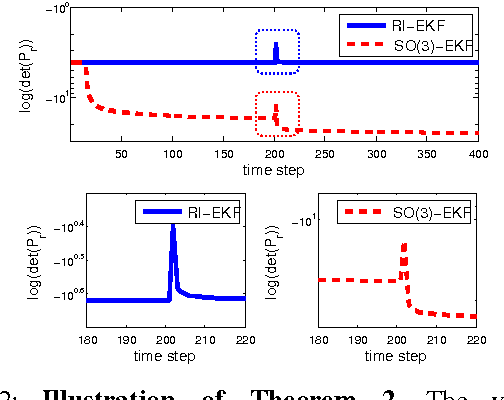
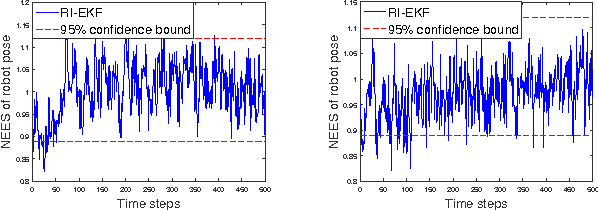
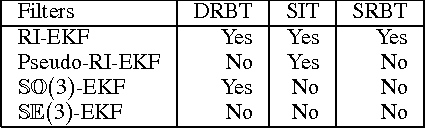
In this paper, we investigate the convergence and consistency properties of an Invariant-Extended Kalman Filter (RI-EKF) based Simultaneous Localization and Mapping (SLAM) algorithm. Basic convergence properties of this algorithm are proven. These proofs do not require the restrictive assumption that the Jacobians of the motion and observation models need to be evaluated at the ground truth. It is also shown that the output of RI-EKF is invariant under any stochastic rigid body transformation in contrast to $\mathbb{SO}(3)$ based EKF SLAM algorithm ($\mathbb{SO}(3)$-EKF) that is only invariant under deterministic rigid body transformation. Implications of these invariance properties on the consistency of the estimator are also discussed. Monte Carlo simulation results demonstrate that RI-EKF outperforms $\mathbb{SO}(3)$-EKF, Robocentric-EKF and the "First Estimates Jacobian" EKF, for 3D point feature based SLAM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge