Consistent and Flexible Selectivity Estimation for High-dimensional Data

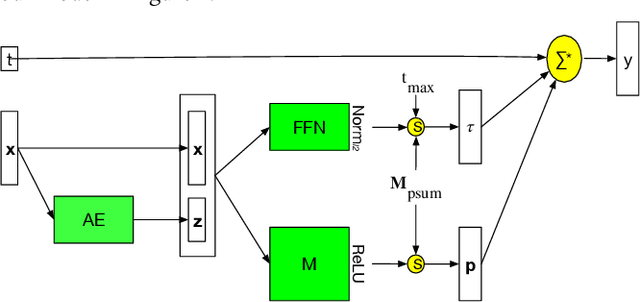
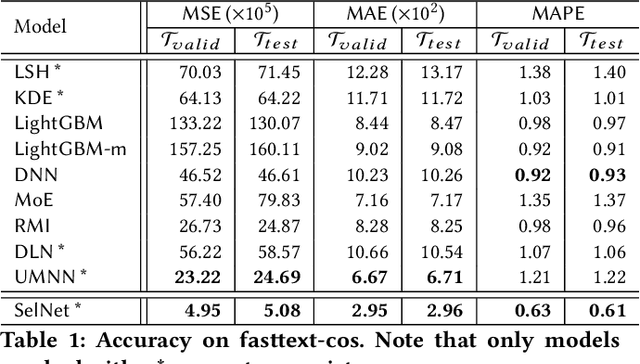
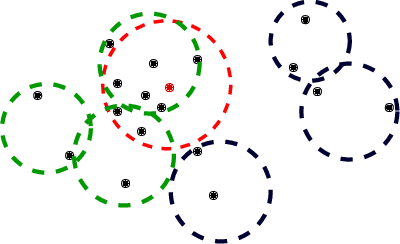
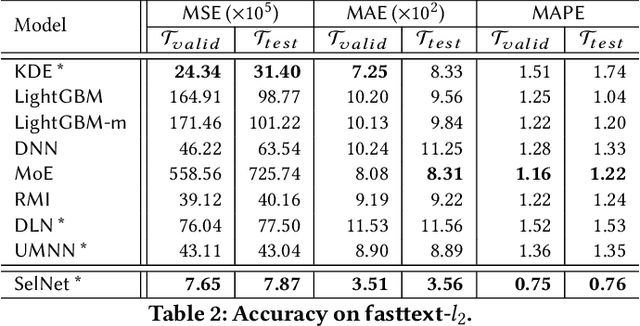
Selectivity estimation aims at estimating the number of database objects that satisfy a selection criterion. Answering this problem accurately and efficiently is essential to applications, such as density estimation, outlier detection, query optimization, and data integration. The estimation problem is especially challenging for large-scale high-dimensional data due to the curse of dimensionality, the need to make the estimator consistent (i.e., the selectivity is non-decreasing w.r.t. the threshold), and the large variance of selectivity across different queries. We propose a new deep learning-based model that learns a query dependent piece-wise linear function as the estimator. We design a novel model architecture so that the model is flexible to fit any selection criterion. To improve the accuracy for large datasets, we propose to divide the dataset into multiple disjoint partitions and build a local model on each of them. We perform experiments on real datasets and show that the proposed model guarantees the consistency and significantly outperforms state-of-the-art models in terms of both accuracy and efficiency.