Computing Capacity-Cost Functions for Continuous Channels in Wasserstein Space
Paper and Code
Jan 18, 2025

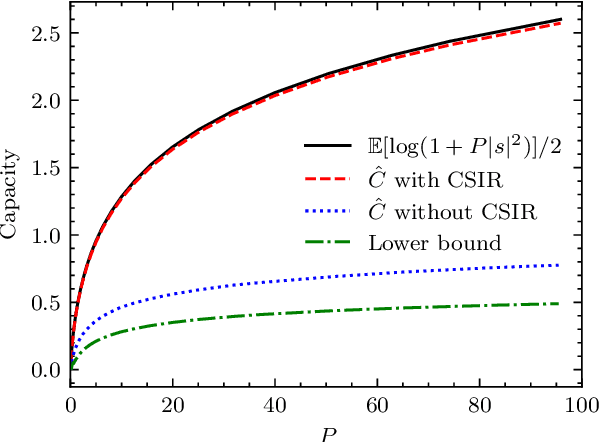
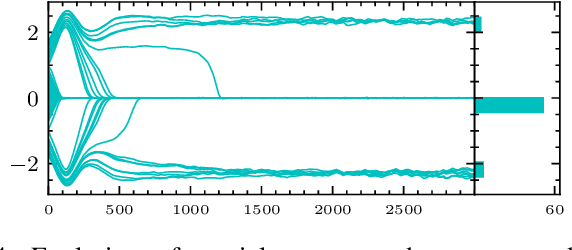
This paper investigates the problem of computing capacity-cost (C-C) functions for continuous channels. Motivated by the Kullback-Leibler divergence (KLD) proximal reformulation of the classical Blahut-Arimoto (BA) algorithm, the Wasserstein distance is introduced to the proximal term for the continuous case, resulting in an iterative algorithm related to the Wasserstein gradient descent. Practical implementation involves moving particles along the negative gradient direction of the objective function's first variation in the Wasserstein space and approximating integrals by the importance sampling (IS) technique. Such formulation is also applied to the rate-distortion (R-D) function for continuous source spaces and thus provides a unified computation framework for both problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge