Compressive Nonparametric Graphical Model Selection For Time Series
Paper and Code
Mar 08, 2014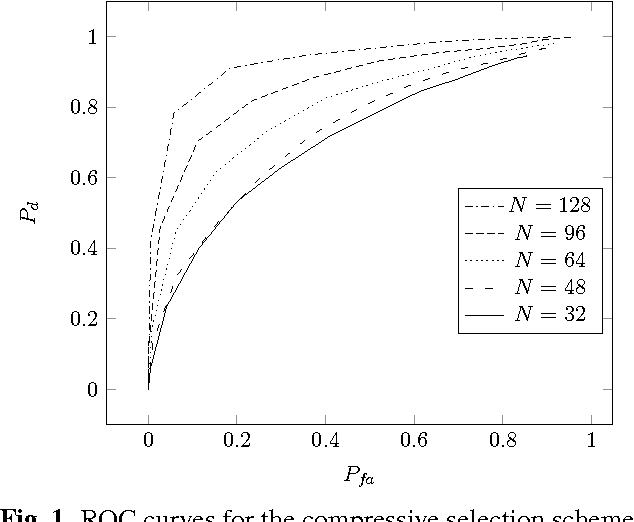
We propose a method for inferring the conditional indepen- dence graph (CIG) of a high-dimensional discrete-time Gaus- sian vector random process from finite-length observations. Our approach does not rely on a parametric model (such as, e.g., an autoregressive model) for the vector random process; rather, it only assumes certain spectral smoothness proper- ties. The proposed inference scheme is compressive in that it works for sample sizes that are (much) smaller than the number of scalar process components. We provide analytical conditions for our method to correctly identify the CIG with high probability.
* to appear in Proc. IEEE ICASSP 2014
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge