Compositional Structures in Neural Embedding and Interaction Decompositions
Paper and Code
Jul 12, 2024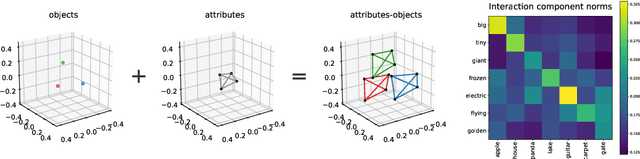
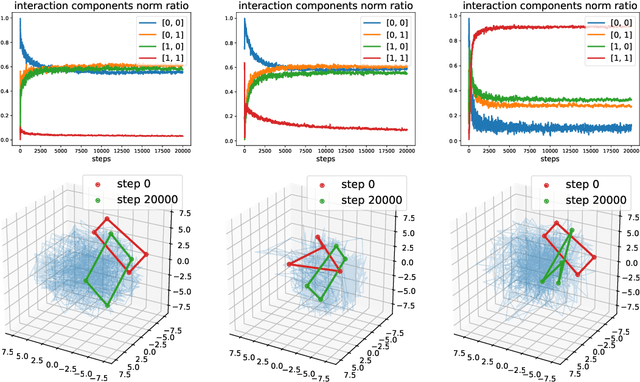
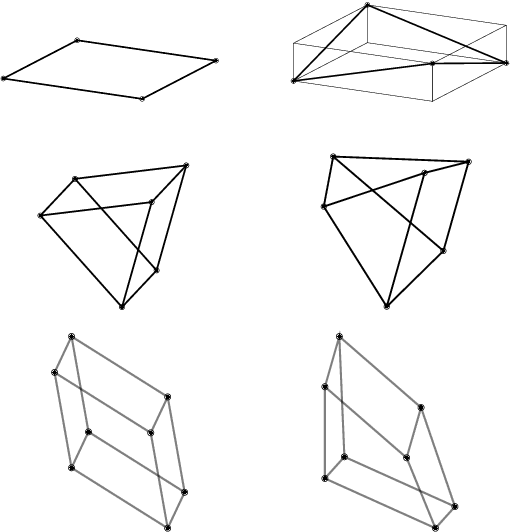
We describe a basic correspondence between linear algebraic structures within vector embeddings in artificial neural networks and conditional independence constraints on the probability distributions modeled by these networks. Our framework aims to shed light on the emergence of structural patterns in data representations, a phenomenon widely acknowledged but arguably still lacking a solid formal grounding. Specifically, we introduce a characterization of compositional structures in terms of "interaction decompositions," and we establish necessary and sufficient conditions for the presence of such structures within the representations of a model.
* 15 pages, 3 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge