COKE: Communication-Censored Kernel Learning for Decentralized Non-parametric Learning

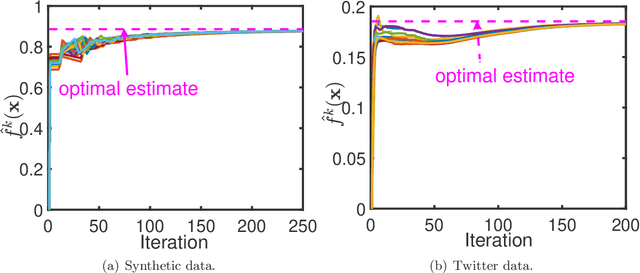
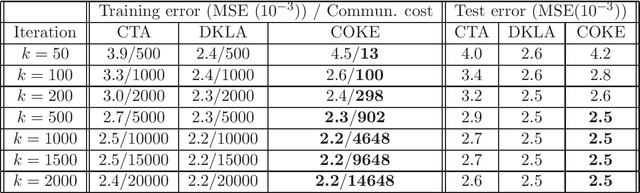
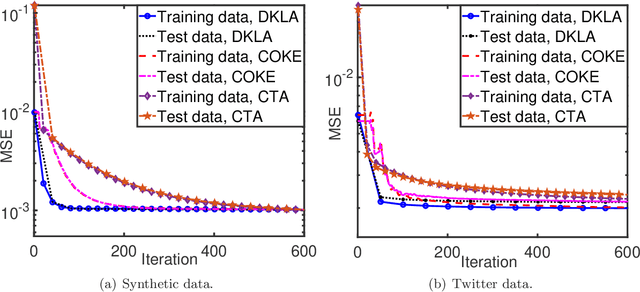
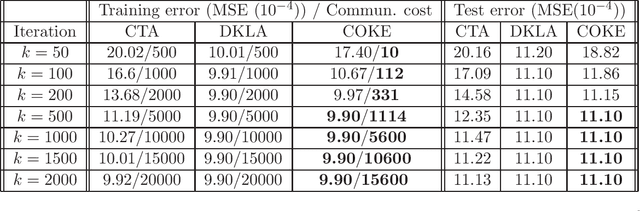
This paper studies the decentralized optimization and learning problem where multiple interconnected agents aim to learn an optimal decision function defined over a reproducing kernel Hilbert (RKH) space by jointly minimizing a global objective function, with access to locally observed data only. As a non-parametric approach, kernel learning faces a major challenge in distributed implementation: the decision variables of local objective functions are data-dependent with different sizes and thus cannot be optimized under the decentralized consensus framework without any raw data exchange among agents. To circumvent this major challenge and preserve data privacy, we leverage the random feature (RF) approximation approach to map the large-volume data represented in the RKH space into a smaller RF space, which facilitates the same-size parameter exchange and enables distributed agents to reach consensus on the function decided by the parameters in the RF space. For fast convergent implementation, we design an iterative algorithm for Decentralized Kernel Learning via Alternating direction method of multipliers (DKLA). Further, we develop a COmmunication-censored KErnel learning (COKE) algorithm to reduce the communication load in DKLA. To do so, we apply a communication-censoring strategy, which prevents an agent from transmitting at every iteration unless its local updates are deemed informative. Theoretical results in terms of linear convergence guarantee and generalization performance analysis of DKLA and COKE are provided. Comprehensive tests with both synthetic and real datasets are conducted to verify the communication efficiency and learning effectiveness of COKE.