CoinPress: Practical Private Mean and Covariance Estimation
Paper and Code
Jun 11, 2020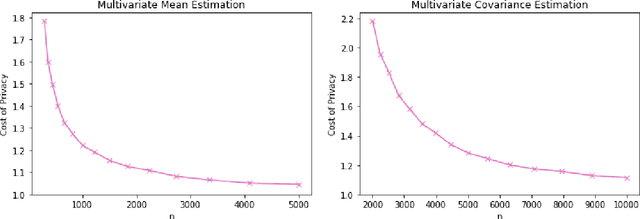
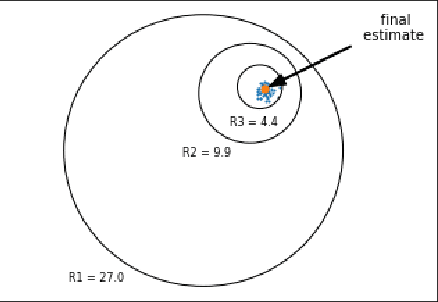
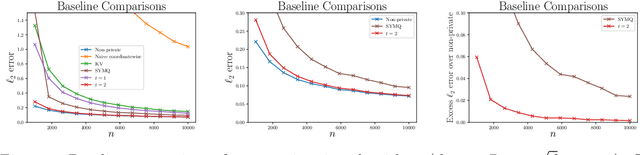
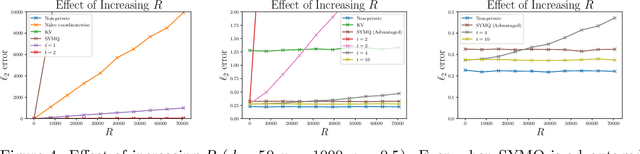
We present simple differentially private estimators for the mean and covariance of multivariate sub-Gaussian data that are accurate at small sample sizes. We demonstrate the effectiveness of our algorithms both theoretically and empirically using synthetic and real-world datasets---showing that their asymptotic error rates match the state-of-the-art theoretical bounds, and that they concretely outperform all previous methods. Specifically, previous estimators either have weak empirical accuracy at small sample sizes, perform poorly for multivariate data, or require the user to provide strong a priori estimates for the parameters.
* Code is available at https://github.com/twistedcubic/coin-press
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge