Clustering by the Probability Distributions from Extreme Value Theory
Paper and Code
Feb 20, 2022
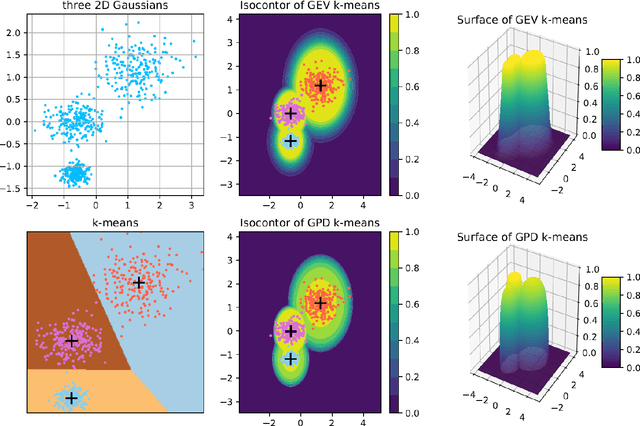

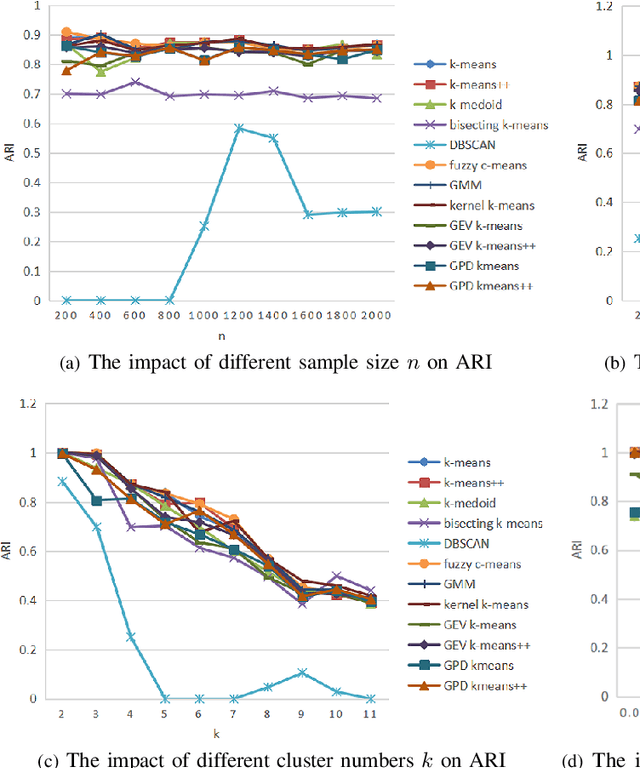
Clustering is an essential task to unsupervised learning. It tries to automatically separate instances into coherent subsets. As one of the most well-known clustering algorithms, k-means assigns sample points at the boundary to a unique cluster, while it does not utilize the information of sample distribution or density. Comparably, it would potentially be more beneficial to consider the probability of each sample in a possible cluster. To this end, this paper generalizes k-means to model the distribution of clusters. Our novel clustering algorithm thus models the distributions of distances to centroids over a threshold by Generalized Pareto Distribution (GPD) in Extreme Value Theory (EVT). Notably, we propose the concept of centroid margin distance, use GPD to establish a probability model for each cluster, and perform a clustering algorithm based on the covering probability function derived from GPD. Such a GPD k-means thus enables the clustering algorithm from the probabilistic perspective. Correspondingly, we also introduce a naive baseline, dubbed as Generalized Extreme Value (GEV) k-means. GEV fits the distribution of the block maxima. In contrast, the GPD fits the distribution of distance to the centroid exceeding a sufficiently large threshold, leading to a more stable performance of GPD k-means. Notably, GEV k-means can also estimate cluster structure and thus perform reasonably well over classical k-means. Thus, extensive experiments on synthetic datasets and real datasets demonstrate that GPD k-means outperforms competitors. The github codes are released in https://github.com/sixiaozheng/EVT-K-means.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge