Chaos is a Ladder: A New Theoretical Understanding of Contrastive Learning via Augmentation Overlap
Paper and Code
Mar 25, 2022
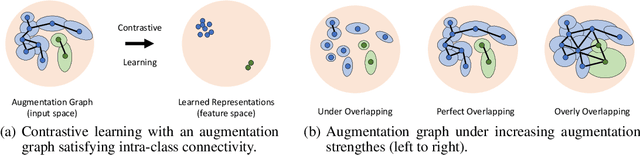
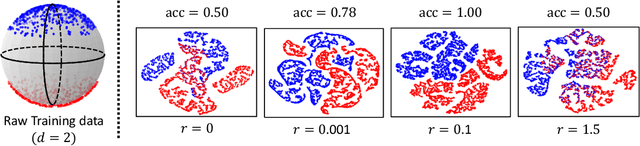
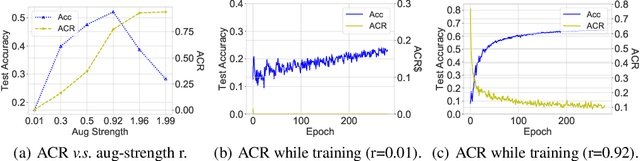
Recently, contrastive learning has risen to be a promising approach for large-scale self-supervised learning. However, theoretical understanding of how it works is still unclear. In this paper, we propose a new guarantee on the downstream performance without resorting to the conditional independence assumption that is widely adopted in previous work but hardly holds in practice. Our new theory hinges on the insight that the support of different intra-class samples will become more overlapped under aggressive data augmentations, thus simply aligning the positive samples (augmented views of the same sample) could make contrastive learning cluster intra-class samples together. Based on this augmentation overlap perspective, theoretically, we obtain asymptotically closed bounds for downstream performance under weaker assumptions, and empirically, we propose an unsupervised model selection metric ARC that aligns well with downstream accuracy. Our theory suggests an alternative understanding of contrastive learning: the role of aligning positive samples is more like a surrogate task than an ultimate goal, and the overlapped augmented views (i.e., the chaos) create a ladder for contrastive learning to gradually learn class-separated representations. The code for computing ARC is available at https://github.com/zhangq327/ARC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge