Causally-motivated Shortcut Removal Using Auxiliary Labels
Paper and Code
Jun 03, 2021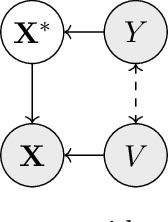

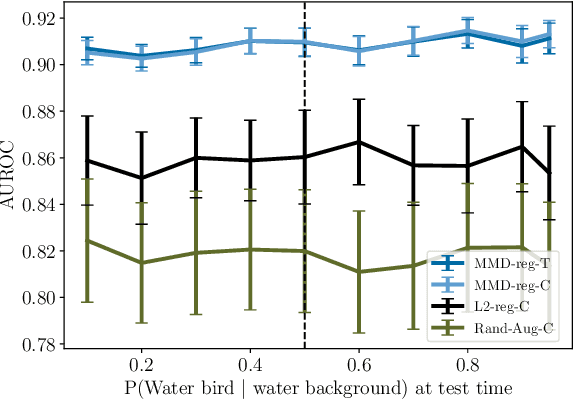
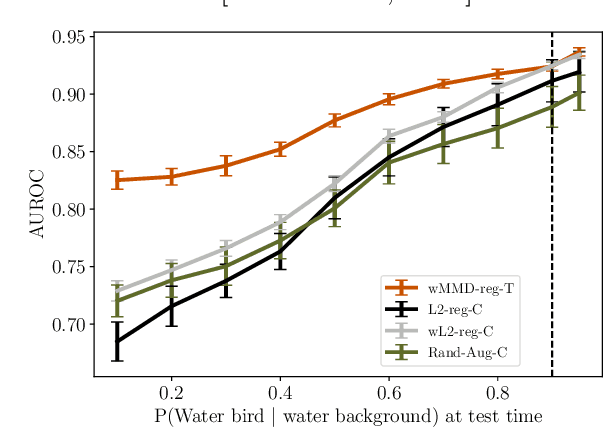
Robustness to certain forms of distribution shift is a key concern in many ML applications. Often, robustness can be formulated as enforcing invariances to particular interventions on the data generating process. Here, we study a flexible, causally-motivated approach to enforcing such invariances, paying special attention to shortcut learning, where a robust predictor can achieve optimal i.i.d generalization in principle, but instead it relies on spurious correlations or shortcuts in practice. Our approach uses auxiliary labels, typically available at training time, to enforce conditional independences between the latent factors that determine these labels. We show both theoretically and empirically that causally-motivated regularization schemes (a) lead to more robust estimators that generalize well under distribution shift, and (b) have better finite sample efficiency compared to usual regularization schemes, even in the absence of distribution shifts. Our analysis highlights important theoretical properties of training techniques commonly used in causal inference, fairness, and disentanglement literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge