Causal Representation Learning from Multiple Distributions: A General Setting
Paper and Code
Feb 07, 2024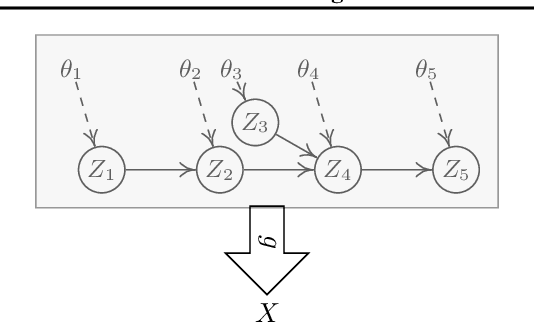
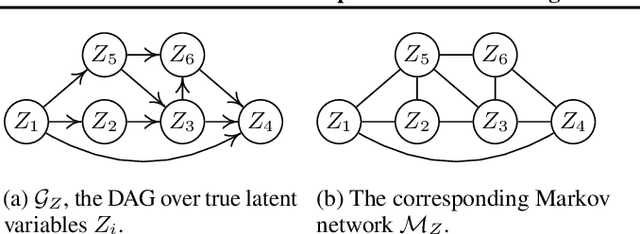
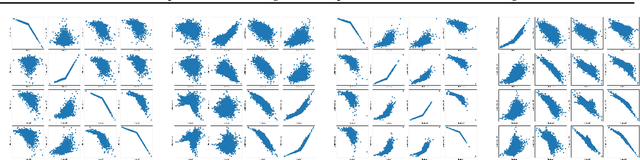
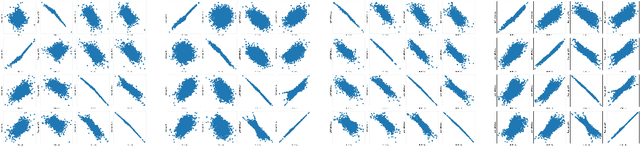
In many problems, the measured variables (e.g., image pixels) are just mathematical functions of the hidden causal variables (e.g., the underlying concepts or objects). For the purpose of making predictions in changing environments or making proper changes to the system, it is helpful to recover the hidden causal variables $Z_i$ and their causal relations represented by graph $\mathcal{G}_Z$. This problem has recently been known as causal representation learning. This paper is concerned with a general, completely nonparametric setting of causal representation learning from multiple distributions (arising from heterogeneous data or nonstationary time series), without assuming hard interventions behind distribution changes. We aim to develop general solutions in this fundamental case; as a by product, this helps see the unique benefit offered by other assumptions such as parametric causal models or hard interventions. We show that under the sparsity constraint on the recovered graph over the latent variables and suitable sufficient change conditions on the causal influences, interestingly, one can recover the moralized graph of the underlying directed acyclic graph, and the recovered latent variables and their relations are related to the underlying causal model in a specific, nontrivial way. In some cases, each latent variable can even be recovered up to component-wise transformations. Experimental results verify our theoretical claims.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge