Budgeted Influence Maximization for Multiple Products
Paper and Code
Apr 16, 2014
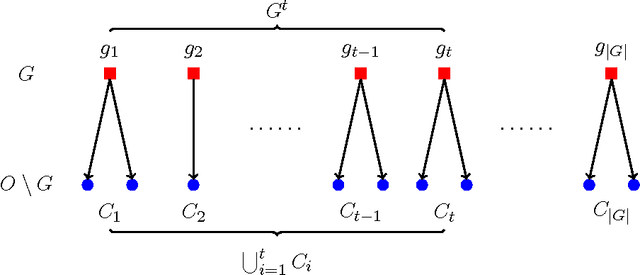
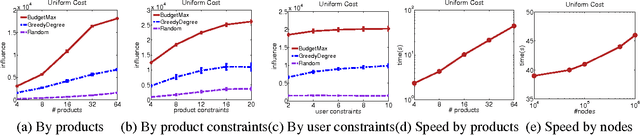
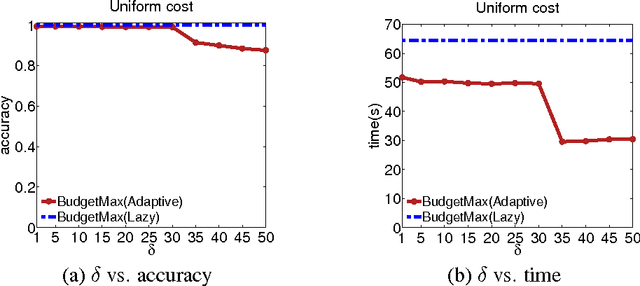
The typical algorithmic problem in viral marketing aims to identify a set of influential users in a social network, who, when convinced to adopt a product, shall influence other users in the network and trigger a large cascade of adoptions. However, the host (the owner of an online social platform) often faces more constraints than a single product, endless user attentions, unlimited budget and unbounded time; in reality, multiple products need to be advertised, each user can tolerate only a small number of recommendations, influencing user has a cost and advertisers have only limited budgets, and the adoptions need to be maximized within a short time window. Given theses myriads of user, monetary, and timing constraints, it is extremely challenging for the host to design principled and efficient viral market algorithms with provable guarantees. In this paper, we provide a novel solution by formulating the problem as a submodular maximization in a continuous-time diffusion model under an intersection of a matroid and multiple knapsack constraints. We also propose an adaptive threshold greedy algorithm which can be faster than the traditional greedy algorithm with lazy evaluation, and scalable to networks with million of nodes. Furthermore, our mathematical formulation allows us to prove that the algorithm can achieve an approximation factor of $k_a/(2+2 k)$ when $k_a$ out of the $k$ knapsack constraints are active, which also improves over previous guarantees from combinatorial optimization literature. In the case when influencing each user has uniform cost, the approximation becomes even better to a factor of $1/3$. Extensive synthetic and real world experiments demonstrate that our budgeted influence maximization algorithm achieves the-state-of-the-art in terms of both effectiveness and scalability, often beating the next best by significant margins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge