Bounding boxes for weakly supervised segmentation: Global constraints get close to full supervision
Paper and Code
Apr 14, 2020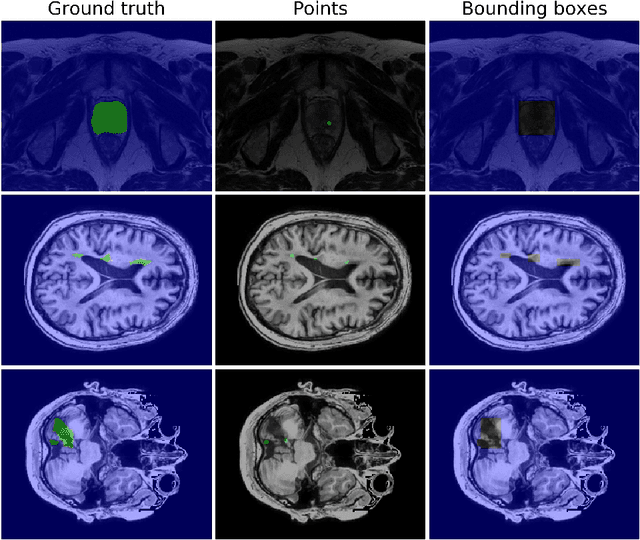
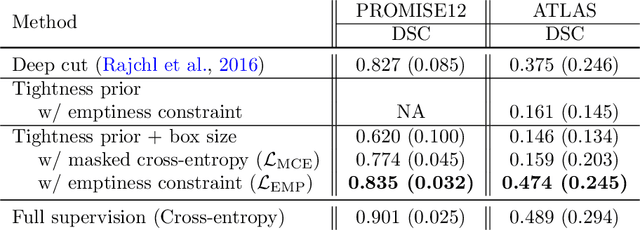
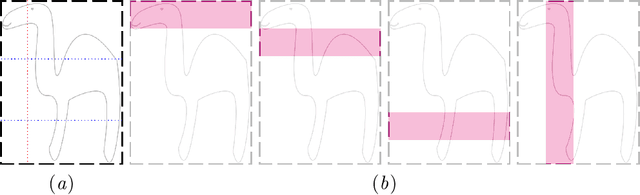

We propose a novel weakly supervised learning segmentation based on several global constraints derived from box annotations. Particularly, we leverage a classical tightness prior to a deep learning setting via imposing a set of constraints on the network outputs. Such a powerful topological prior prevents solutions from excessive shrinking by enforcing any horizontal or vertical line within the bounding box to contain, at least, one pixel of the foreground region. Furthermore, we integrate our deep tightness prior with a global background emptiness constraint, guiding training with information outside the bounding box. We demonstrate experimentally that such a global constraint is much more powerful than standard cross-entropy for the background class. Our optimization problem is challenging as it takes the form of a large set of inequality constraints on the outputs of deep networks. We solve it with sequence of unconstrained losses based on a recent powerful extension of the log-barrier method, which is well-known in the context of interior-point methods. This accommodates standard stochastic gradient descent (SGD) for training deep networks, while avoiding computationally expensive and unstable Lagrangian dual steps and projections. Extensive experiments over two different public data sets and applications (prostate and brain lesions) demonstrate that the synergy between our global tightness and emptiness priors yield very competitive performances, approaching full supervision and outperforming significantly DeepCut. Furthermore, our approach removes the need for computationally expensive proposal generation. Our code is shared anonymously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge