Block-wise Dynamic Sparseness
Paper and Code
Jan 14, 2020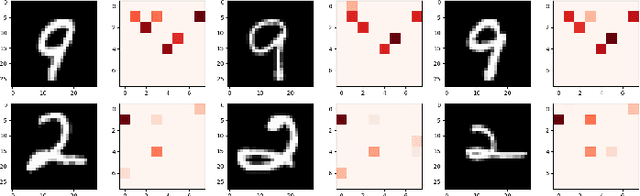
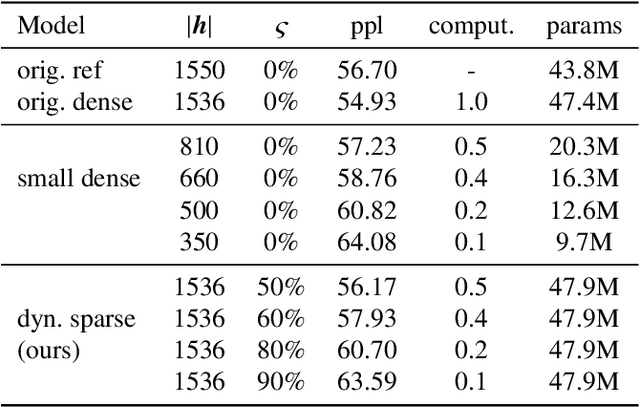
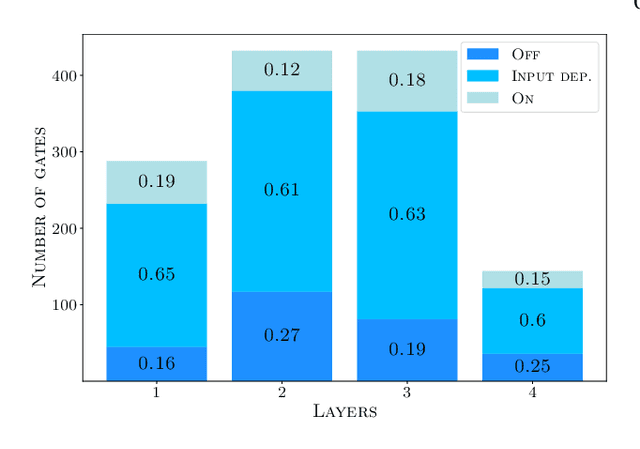
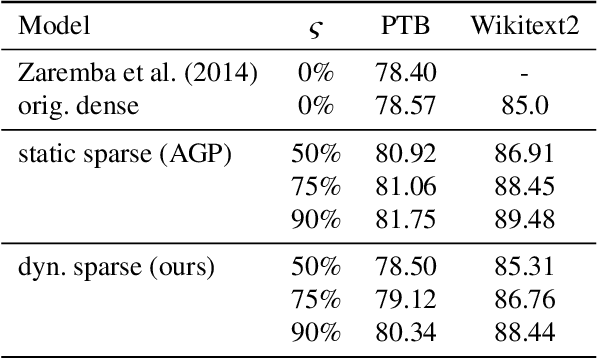
Neural networks have achieved state of the art performance across a wide variety of machine learning tasks, often with large and computation-heavy models. Inducing sparseness as a way to reduce the memory and computation footprint of these models has seen significant research attention in recent years. In this paper, we present a new method for \emph{dynamic sparseness}, whereby part of the computations are omitted dynamically, based on the input. For efficiency, we combined the idea of dynamic sparseness with block-wise matrix-vector multiplications. In contrast to static sparseness, which permanently zeroes out selected positions in weight matrices, our method preserves the full network capabilities by potentially accessing any trained weights. Yet, matrix vector multiplications are accelerated by omitting a pre-defined fraction of weight blocks from the matrix, based on the input. Experimental results on the task of language modeling, using recurrent and quasi-recurrent models, show that the proposed method can outperform a magnitude-based static sparseness baseline. In addition, our method achieves similar language modeling perplexities as the dense baseline, at half the computational cost at inference time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge