Black-Box Complexities of Combinatorial Problems

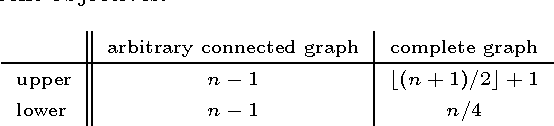
Black-box complexity is a complexity theoretic measure for how difficult a problem is to be optimized by a general purpose optimization algorithm. It is thus one of the few means trying to understand which problems are tractable for genetic algorithms and other randomized search heuristics. Most previous work on black-box complexity is on artificial test functions. In this paper, we move a step forward and give a detailed analysis for the two combinatorial problems minimum spanning tree and single-source shortest paths. Besides giving interesting bounds for their black-box complexities, our work reveals that the choice of how to model the optimization problem is non-trivial here. This in particular comes true where the search space does not consist of bit strings and where a reasonable definition of unbiasedness has to be agreed on.