BitNet: Bit-Regularized Deep Neural Networks
Paper and Code
Jun 26, 2018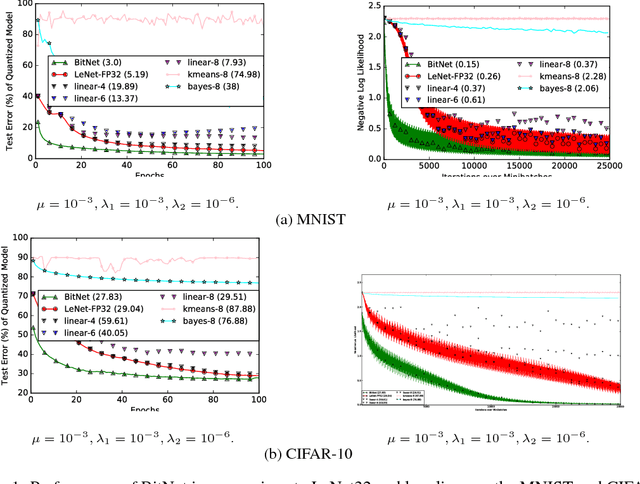
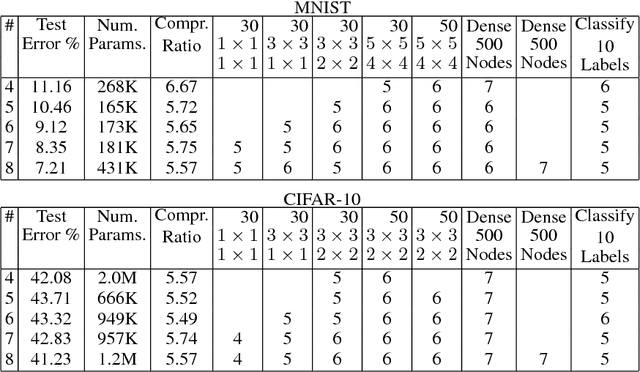
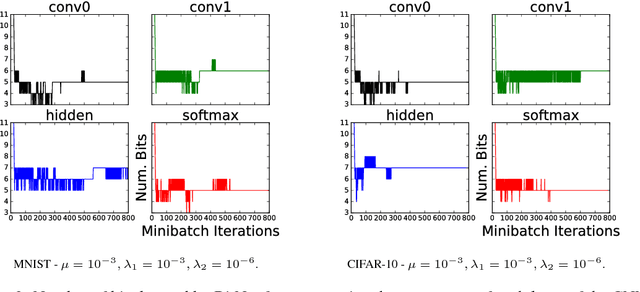
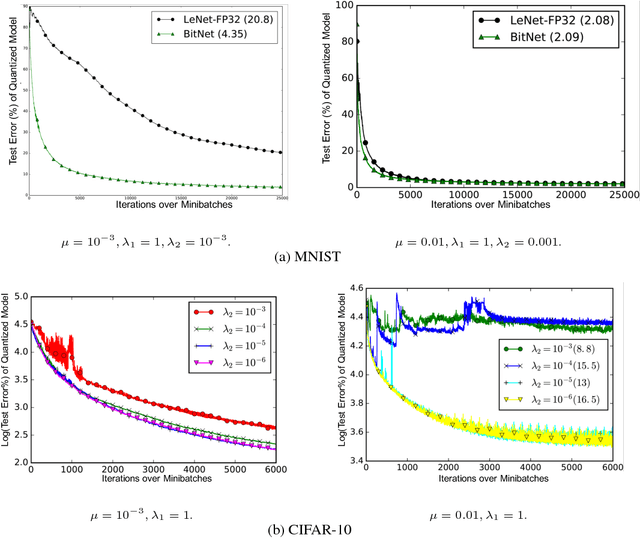
We present a novel optimization strategy for training neural networks which we call "BitNet". The parameters of neural networks are usually unconstrained and have a dynamic range dispersed over all real values. Our key idea is to limit the expressive power of the network by dynamically controlling the range and set of values that the parameters can take. We formulate this idea using a novel end-to-end approach that circumvents the discrete parameter space by optimizing a relaxed continuous and differentiable upper bound of the typical classification loss function. The approach can be interpreted as a regularization inspired by the Minimum Description Length (MDL) principle. For each layer of the network, our approach optimizes real-valued translation and scaling factors and arbitrary precision integer-valued parameters (weights). We empirically compare BitNet to an equivalent unregularized model on the MNIST and CIFAR-10 datasets. We show that BitNet converges faster to a superior quality solution. Additionally, the resulting model has significant savings in memory due to the use of integer-valued parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge