Bipartite Conditional Random Fields for Panoptic Segmentation
Paper and Code
Dec 11, 2019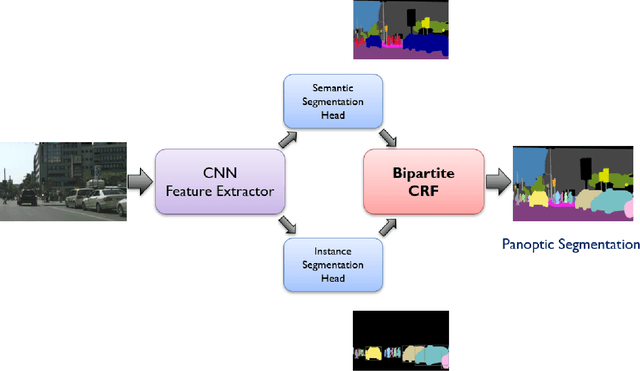
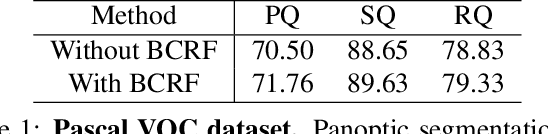
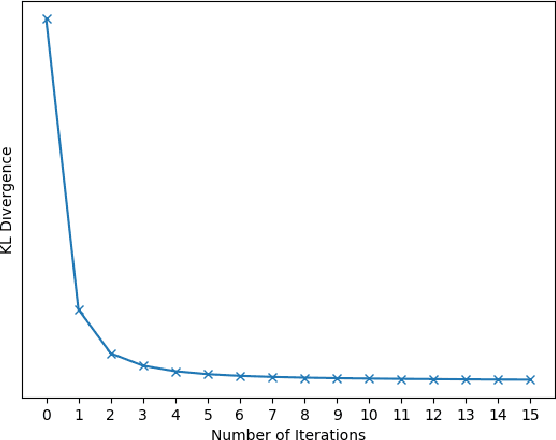

We tackle the panoptic segmentation problem with a conditional random field (CRF) model. Panoptic segmentation involves assigning a semantic label and an instance label to each pixel of a given image. At each pixel, the semantic label and the instance label should be compatible. Furthermore, a good panoptic segmentation should have a number of other desirable properties such as the spatial and color consistency of the labeling (similar looking neighboring pixels should have the same semantic label and the instance label). To tackle this problem, we propose a CRF model, named Bipartite CRF or BCRF, with two types of random variables for semantic and instance labels. In this formulation, various energies are defined within and across the two types of random variables to encourage a consistent panoptic segmentation. We propose a mean-field-based efficient inference algorithm for solving the CRF and empirically show its convergence properties. This algorithm is fully differentiable, and therefore, BCRF inference can be included as a trainable module in a deep network. In the experimental evaluation, we quantitatively and qualitatively show that the BCRF yields superior panoptic segmentation results in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge