Beyond $\mathcal{H}$-Divergence: Domain Adaptation Theory With Jensen-Shannon Divergence
Paper and Code
Jul 30, 2020

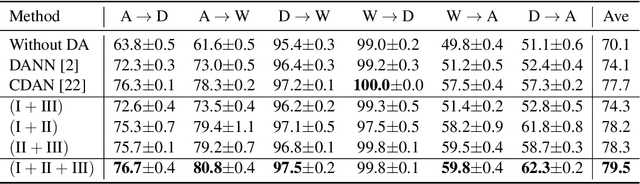
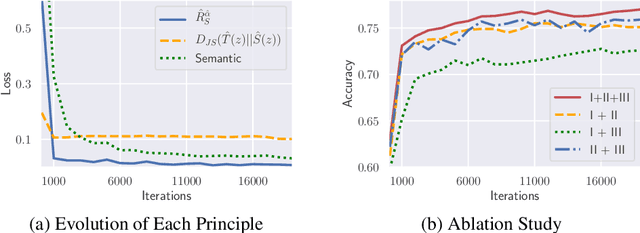
We reveal the incoherence between the widely-adopted empirical domain adversarial training and its generally-assumed theoretical counterpart based on $\mathcal{H}$-divergence. Concretely, we find that $\mathcal{H}$-divergence is not equivalent to Jensen-Shannon divergence, the optimization objective in domain adversarial training. To this end, we establish a new theoretical framework by directly proving the upper and lower target risk bounds based on joint distributional Jensen-Shannon divergence. We further derive bi-directional upper bounds for marginal and conditional shifts. Our framework exhibits inherent flexibilities for different transfer learning problems, which is usable for various scenarios where $\mathcal{H}$-divergence-based theory fails to adapt. From an algorithmic perspective, our theory enables a generic guideline unifying principles of semantic conditional matching, feature marginal matching, and label marginal shift correction. We employ algorithms for each principle and empirically validate the benefits of our framework on real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge