Benefits of Permutation-Equivariance in Auction Mechanisms
Paper and Code
Oct 11, 2022


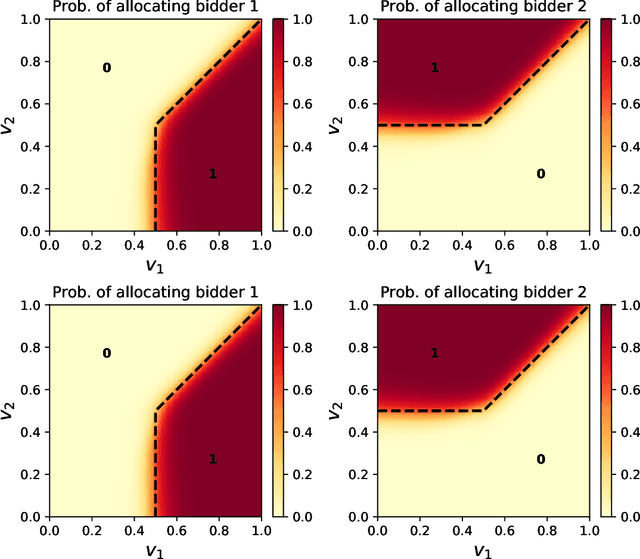
Designing an incentive-compatible auction mechanism that maximizes the auctioneer's revenue while minimizes the bidders' ex-post regret is an important yet intricate problem in economics. Remarkable progress has been achieved through learning the optimal auction mechanism by neural networks. In this paper, we consider the popular additive valuation and symmetric valuation setting; i.e., the valuation for a set of items is defined as the sum of all items' valuations in the set, and the valuation distribution is invariant when the bidders and/or the items are permutated. We prove that permutation-equivariant neural networks have significant advantages: the permutation-equivariance decreases the expected ex-post regret, improves the model generalizability, while maintains the expected revenue invariant. This implies that the permutation-equivariance helps approach the theoretically optimal dominant strategy incentive compatible condition, and reduces the required sample complexity for desired generalization. Extensive experiments fully support our theory. To our best knowledge, this is the first work towards understanding the benefits of permutation-equivariance in auction mechanisms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge