Belief-selective Propagation Detection for MIMO Systems
Paper and Code
Jun 27, 2022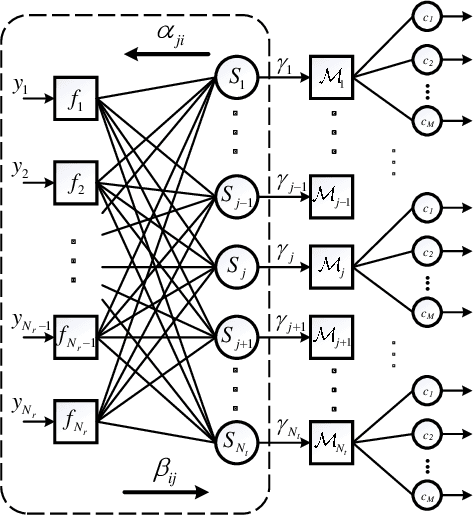
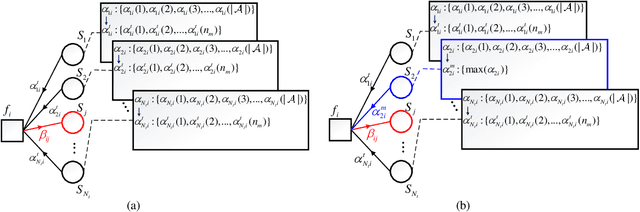
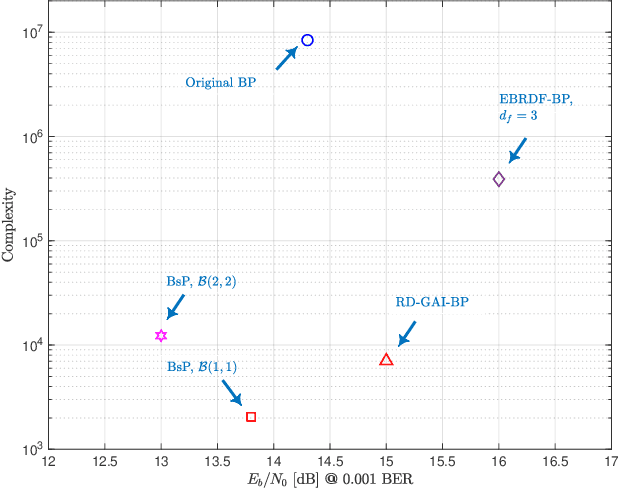
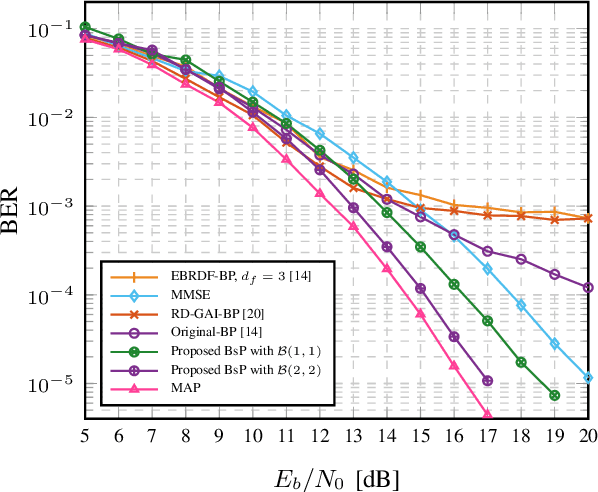
Compared to the linear MIMO detectors, the Belief Propagation (BP) detector has shown greater capabilities in achieving near optimal performance and better nature to iteratively cooperate with channel decoders. Aiming at real applications, recent works mainly fall into the category of reducing the complexity by simplified calculations, at the expense of performance sacrifice. However, the complexity is still unsatisfactory with exponentially increasing complexity or required exponentiation operations. Furthermore, due to the inherent loopy structure, the existing BP detectors persistently encounter error floor in high signal-to-noise ratio (SNR) region, which becomes even worse with calculation approximation. This work aims at a revised BP detector, named {Belief-selective Propagation (BsP)} detector by selectively utilizing the \emph{trusted} incoming messages with sufficiently large \textit{a priori} probabilities for updates. Two proposed strategies: symbol-based truncation (ST) and edge-based simplification (ES) squeeze the complexity (orders lower than the Original-BP), while greatly relieving the error floor issue over a wide range of antenna and modulation combinations. For the $16$-QAM $8 \times 4$ MIMO system, the $\mathcal{B}(1,1)$ {BsP} detector achieves more than $4$\,dB performance gain (@$\text{BER}=10^{-4}$) with roughly $4$ orders lower complexity than the Original-BP detector. Trade-off between performance and complexity towards different application requirement can be conveniently obtained by configuring the ST and ES parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge