Bargaining for Revenue Shares on Tree Trading Networks
Paper and Code
Apr 22, 2013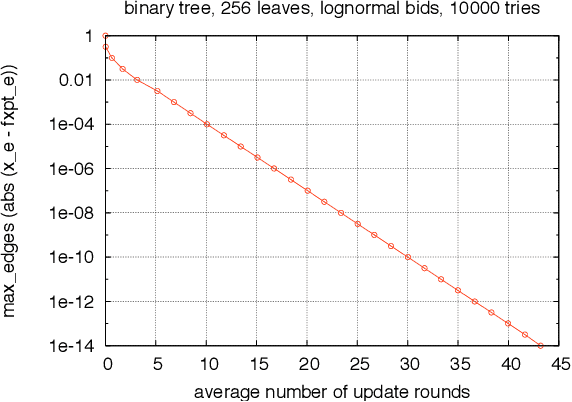
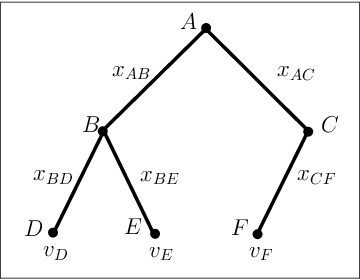
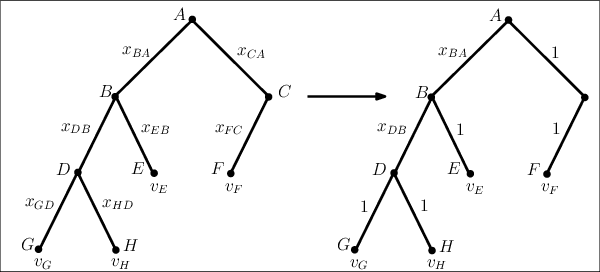
We study trade networks with a tree structure, where a seller with a single indivisible good is connected to buyers, each with some value for the good, via a unique path of intermediaries. Agents in the tree make multiplicative revenue share offers to their parent nodes, who choose the best offer and offer part of it to their parent, and so on; the winning path is determined by who finally makes the highest offer to the seller. In this paper, we investigate how these revenue shares might be set via a natural bargaining process between agents on the tree, specifically, egalitarian bargaining between endpoints of each edge in the tree. We investigate the fixed point of this system of bargaining equations and prove various desirable for this solution concept, including (i) existence, (ii) uniqueness, (iii) efficiency, (iv) membership in the core, (v) strict monotonicity, (vi) polynomial-time computability to any given accuracy. Finally, we present numerical evidence that asynchronous dynamics with randomly ordered updates always converges to the fixed point, indicating that the fixed point shares might arise from decentralized bargaining amongst agents on the trade network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge