AVT: Unsupervised Learning of Transformation Equivariant Representations by Autoencoding Variational Transformations

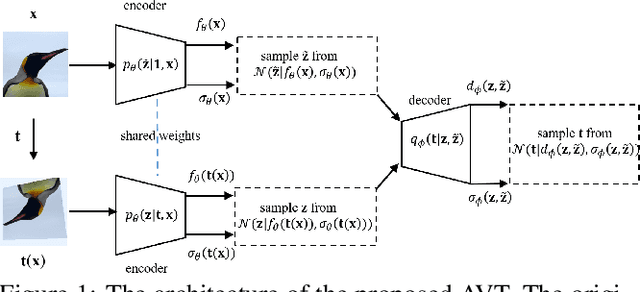
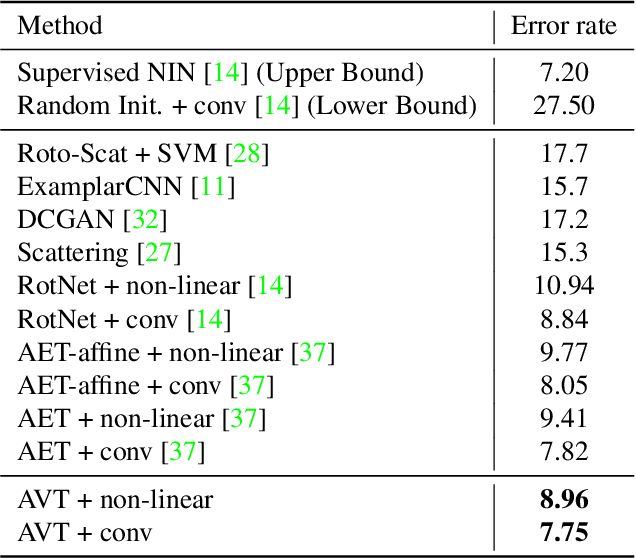
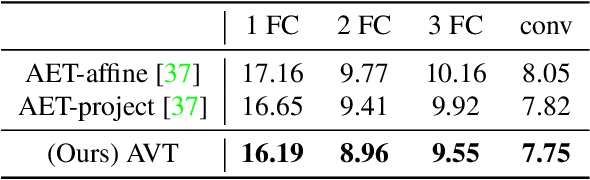
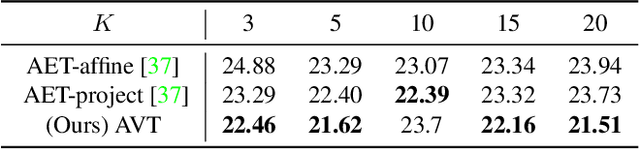
The learning of Transformation-Equivariant Representations (TERs), which is introduced by Hinton et al. \cite{hinton2011transforming}, has been considered as a principle to reveal visual structures under various transformations. It contains the celebrated Convolutional Neural Networks (CNNs) as a special case that only equivary to the translations. In contrast, we seek to train TERs for a generic class of transformations and train them in an {\em unsupervised} fashion. To this end, we present a novel principled method by Autoencoding Variational Transformations (AVT), compared with the conventional approach to autoencoding data. Formally, given transformed images, the AVT seeks to train the networks by maximizing the mutual information between the transformations and representations. This ensures the resultant TERs of individual images contain the {\em intrinsic} information about their visual structures that would equivary {\em extricably} under various transformations. Technically, we show that the resultant optimization problem can be efficiently solved by maximizing a variational lower-bound of the mutual information. This variational approach introduces a transformation decoder to approximate the intractable posterior of transformations, resulting in an autoencoding architecture with a pair of the representation encoder and the transformation decoder. Experiments demonstrate the proposed AVT model sets a new record for the performances on unsupervised tasks, greatly closing the performance gap to the supervised models.