Automatic Variational ABC
Paper and Code
Jun 28, 2016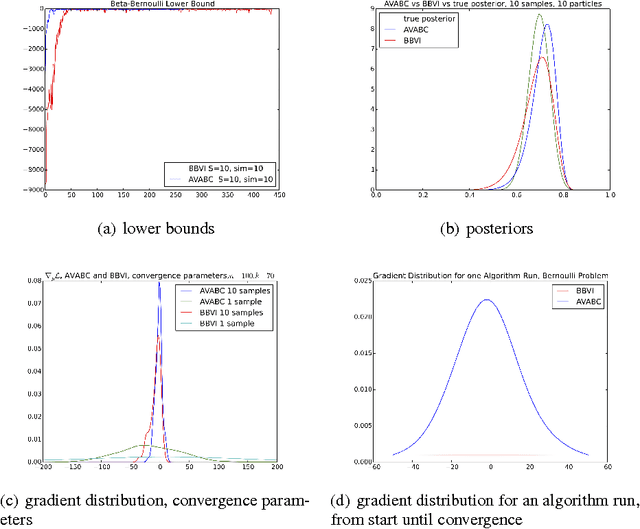
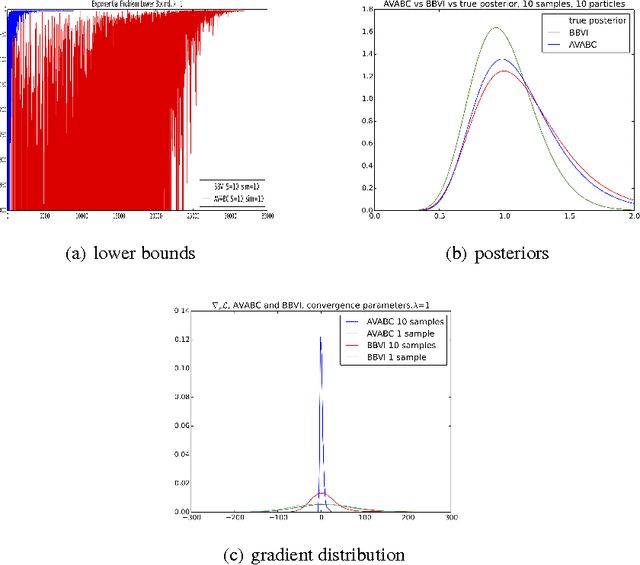
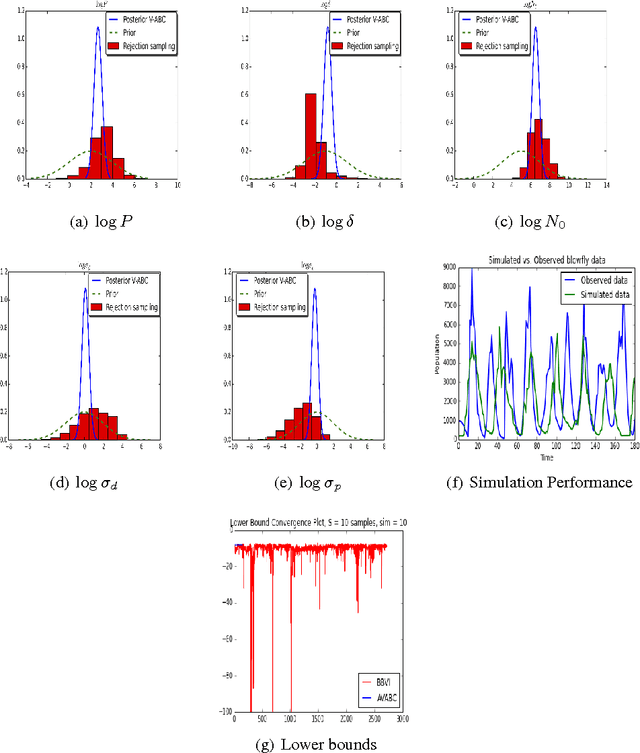
Approximate Bayesian Computation (ABC) is a framework for performing likelihood-free posterior inference for simulation models. Stochastic Variational inference (SVI) is an appealing alternative to the inefficient sampling approaches commonly used in ABC. However, SVI is highly sensitive to the variance of the gradient estimators, and this problem is exacerbated by approximating the likelihood. We draw upon recent advances in variance reduction for SV and likelihood-free inference using deterministic simulations to produce low variance gradient estimators of the variational lower-bound. By then exploiting automatic differentiation libraries we can avoid nearly all model-specific derivations. We demonstrate performance on three problems and compare to existing SVI algorithms. Our results demonstrate the correctness and efficiency of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge