Automatic Discovery of Privacy-Utility Pareto Fronts
Paper and Code
May 26, 2019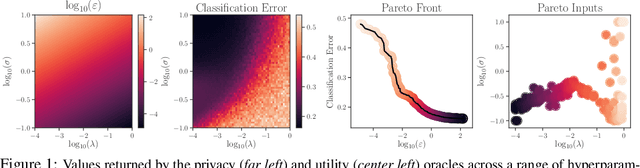
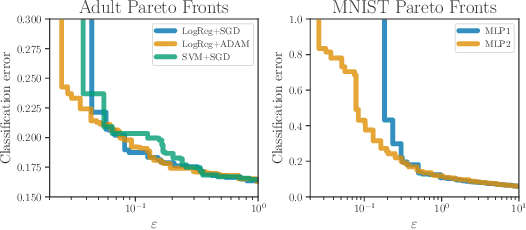
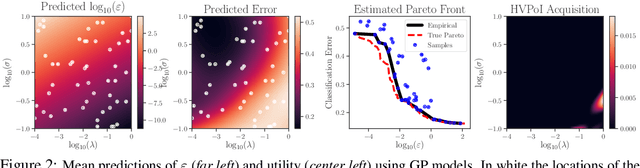

Differential privacy is a mathematical framework for privacy-preserving data analysis. Changing the hyperparameters of a differentially private algorithm allows one to trade off privacy and utility in a principled way. Quantifying this trade-off in advance is essential to decision-makers tasked with deciding how much privacy can be provided in a particular application while keeping acceptable utility. For more complex tasks, such as training neural networks under differential privacy, the utility achieved by a given algorithm can only be measured empirically. This paper presents a Bayesian optimization methodology for efficiently characterizing the privacy-utility trade-off of any differentially private algorithm using only empirical measurements of its utility. The versatility of our method is illustrated on a number of machine learning tasks involving multiple models, optimizers, and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge