Asynchronous Training Schemes in Distributed Learning with Time Delay
Paper and Code
Aug 28, 2022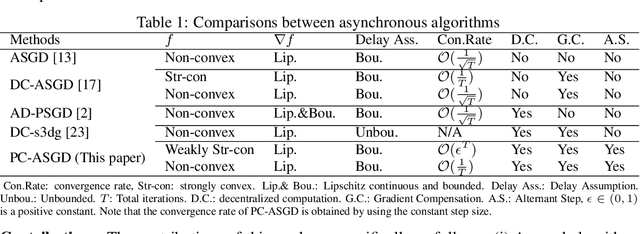
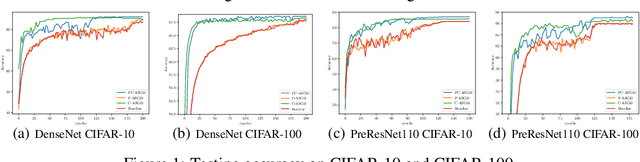

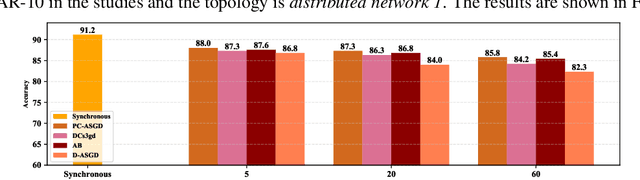
In the context of distributed deep learning, the issue of stale weights or gradients could result in poor algorithmic performance. This issue is usually tackled by delay tolerant algorithms with some mild assumptions on the objective functions and step sizes. In this paper, we propose a different approach to develop a new algorithm, called $\textbf{P}$redicting $\textbf{C}$lipping $\textbf{A}$synchronous $\textbf{S}$tochastic $\textbf{G}$radient $\textbf{D}$escent (aka, PC-ASGD). Specifically, PC-ASGD has two steps - the $\textit{predicting step}$ leverages the gradient prediction using Taylor expansion to reduce the staleness of the outdated weights while the $\textit{clipping step}$ selectively drops the outdated weights to alleviate their negative effects. A tradeoff parameter is introduced to balance the effects between these two steps. Theoretically, we present the convergence rate considering the effects of delay of the proposed algorithm with constant step size when the smooth objective functions are weakly strongly-convex and nonconvex. One practical variant of PC-ASGD is also proposed by adopting a condition to help with the determination of the tradeoff parameter. For empirical validation, we demonstrate the performance of the algorithm with two deep neural network architectures on two benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge