Asynchronous Stochastic Proximal Optimization Algorithms with Variance Reduction
Paper and Code
Sep 27, 2016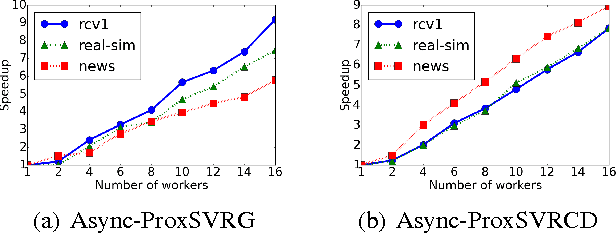

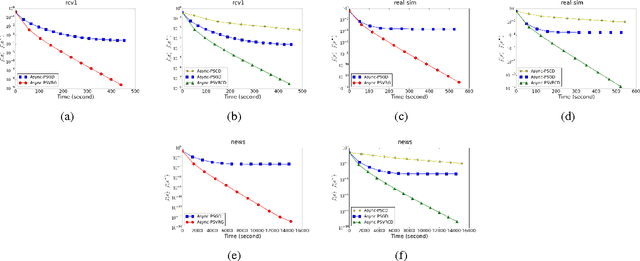
Regularized empirical risk minimization (R-ERM) is an important branch of machine learning, since it constrains the capacity of the hypothesis space and guarantees the generalization ability of the learning algorithm. Two classic proximal optimization algorithms, i.e., proximal stochastic gradient descent (ProxSGD) and proximal stochastic coordinate descent (ProxSCD) have been widely used to solve the R-ERM problem. Recently, variance reduction technique was proposed to improve ProxSGD and ProxSCD, and the corresponding ProxSVRG and ProxSVRCD have better convergence rate. These proximal algorithms with variance reduction technique have also achieved great success in applications at small and moderate scales. However, in order to solve large-scale R-ERM problems and make more practical impacts, the parallel version of these algorithms are sorely needed. In this paper, we propose asynchronous ProxSVRG (Async-ProxSVRG) and asynchronous ProxSVRCD (Async-ProxSVRCD) algorithms, and prove that Async-ProxSVRG can achieve near linear speedup when the training data is sparse, while Async-ProxSVRCD can achieve near linear speedup regardless of the sparse condition, as long as the number of block partitions are appropriately set. We have conducted experiments on a regularized logistic regression task. The results verified our theoretical findings and demonstrated the practical efficiency of the asynchronous stochastic proximal algorithms with variance reduction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge