Are High-Degree Representations Really Unnecessary in Equivariant Graph Neural Networks?
Paper and Code
Oct 15, 2024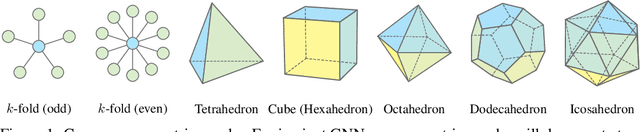
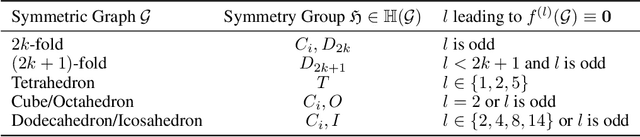
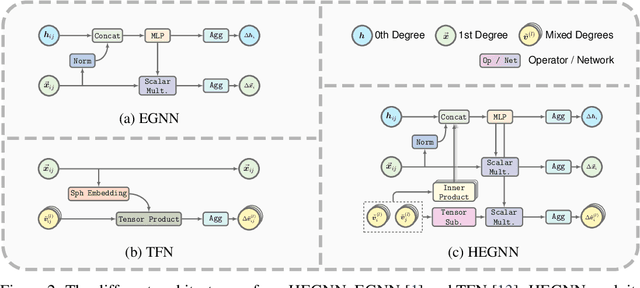
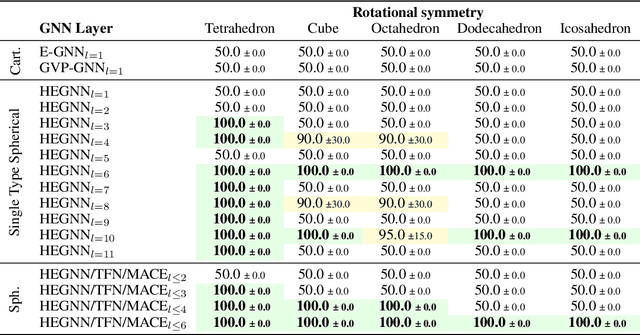
Equivariant Graph Neural Networks (GNNs) that incorporate E(3) symmetry have achieved significant success in various scientific applications. As one of the most successful models, EGNN leverages a simple scalarization technique to perform equivariant message passing over only Cartesian vectors (i.e., 1st-degree steerable vectors), enjoying greater efficiency and efficacy compared to equivariant GNNs using higher-degree steerable vectors. This success suggests that higher-degree representations might be unnecessary. In this paper, we disprove this hypothesis by exploring the expressivity of equivariant GNNs on symmetric structures, including $k$-fold rotations and regular polyhedra. We theoretically demonstrate that equivariant GNNs will always degenerate to a zero function if the degree of the output representations is fixed to 1 or other specific values. Based on this theoretical insight, we propose HEGNN, a high-degree version of EGNN to increase the expressivity by incorporating high-degree steerable vectors while maintaining EGNN's efficiency through the scalarization trick. Our extensive experiments demonstrate that HEGNN not only aligns with our theoretical analyses on toy datasets consisting of symmetric structures, but also shows substantial improvements on more complicated datasets such as $N$-body and MD17. Our theoretical findings and empirical results potentially open up new possibilities for the research of equivariant GNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge