Arbitrary Decisions are a Hidden Cost of Differentially-Private Training
Paper and Code
Feb 28, 2023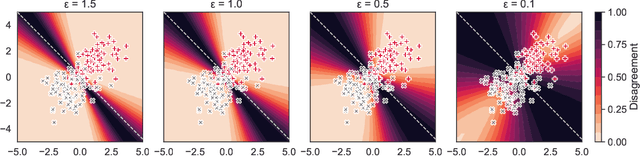
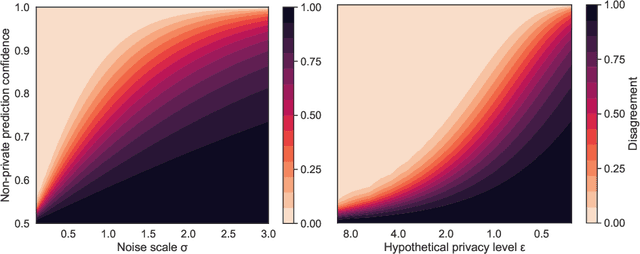
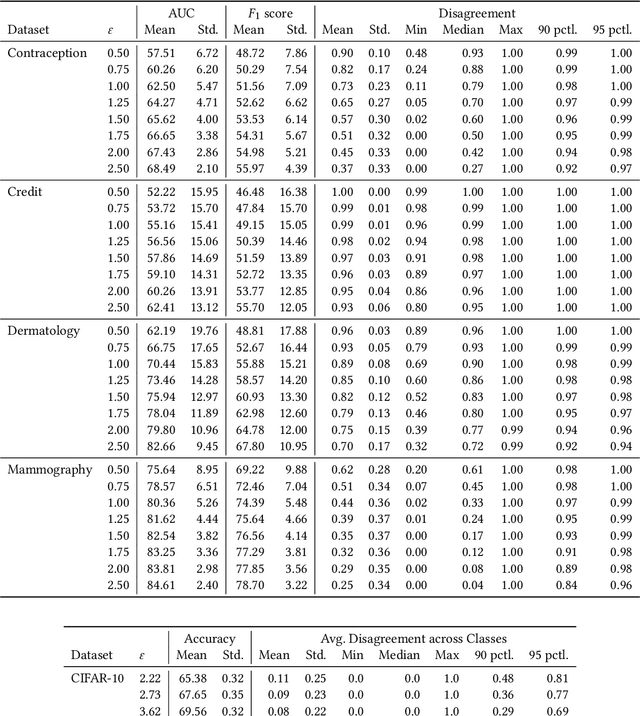
Mechanisms used in privacy-preserving machine learning often aim to guarantee differential privacy (DP) during model training. Practical DP-ensuring training methods use randomization when fitting model parameters to privacy-sensitive data (e.g., adding Gaussian noise to clipped gradients). We demonstrate that such randomization incurs predictive multiplicity: for a given input example, the output predicted by equally-private models depends on the randomness used in training. Thus, for a given input, the predicted output can vary drastically if a model is re-trained, even if the same training dataset is used. The predictive-multiplicity cost of DP training has not been studied, and is currently neither audited for nor communicated to model designers and stakeholders. We derive a bound on the number of re-trainings required to estimate predictive multiplicity reliably. We analyze -- both theoretically and through extensive experiments -- the predictive-multiplicity cost of three DP-ensuring algorithms: output perturbation, objective perturbation, and DP-SGD. We demonstrate that the degree of predictive multiplicity rises as the level of privacy increases, and is unevenly distributed across individuals and demographic groups in the data. Because randomness used to ensure DP during training explains predictions for some examples, our results highlight a fundamental challenge to the justifiability of decisions supported by differentially-private models in high-stakes settings. We conclude that practitioners should audit the predictive multiplicity of their DP-ensuring algorithms before deploying them in applications of individual-level consequence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge