Approximate Top-$k$ for Increased Parallelism
Paper and Code
Dec 05, 2024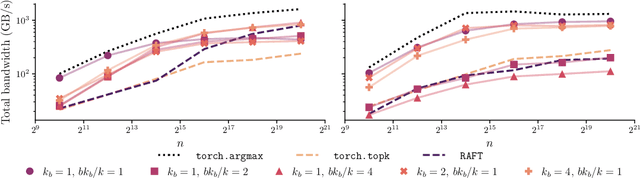
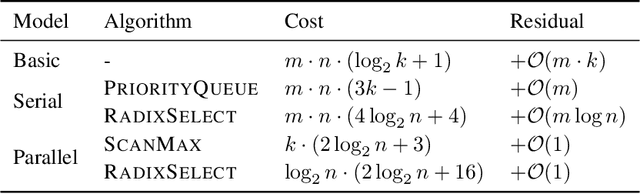
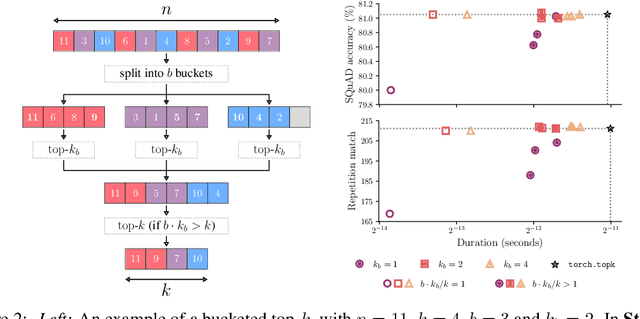
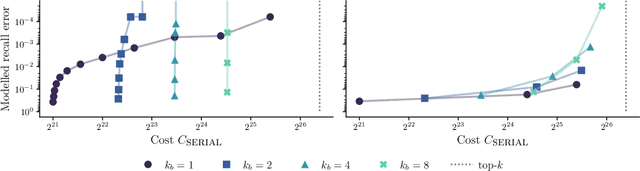
We present an evaluation of bucketed approximate top-$k$ algorithms. Computing top-$k$ exactly suffers from limited parallelism, because the $k$ largest values must be aggregated along the vector, thus is not well suited to computation on highly-parallel machine learning accelerators. By relaxing the requirement that the top-$k$ is exact, bucketed algorithms can dramatically increase the parallelism available by independently computing many smaller top-$k$ operations. We explore the design choices of this class of algorithms using both theoretical analysis and empirical evaluation on downstream tasks. Our motivating examples are sparsity algorithms for language models, which often use top-$k$ to select the most important parameters or activations. We also release a fast bucketed top-$k$ implementation for PyTorch.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge