Anticorrelated Noise Injection for Improved Generalization
Paper and Code
Feb 06, 2022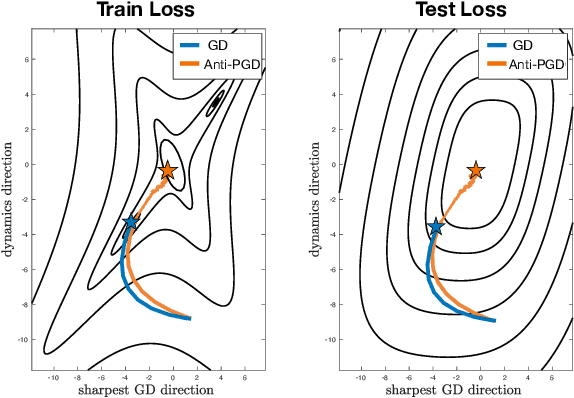
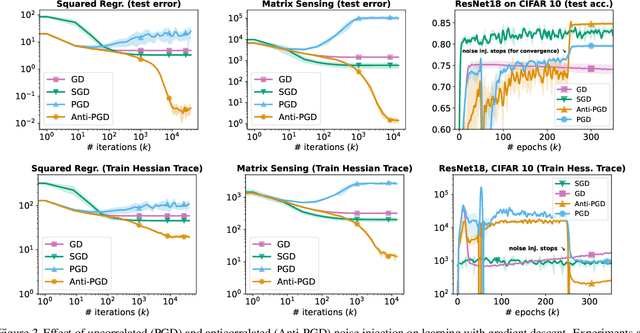
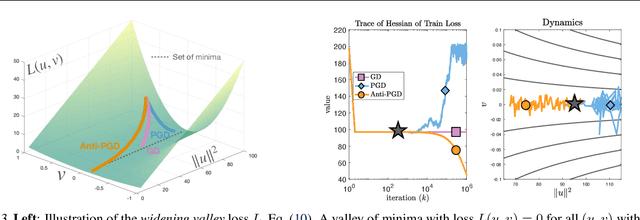
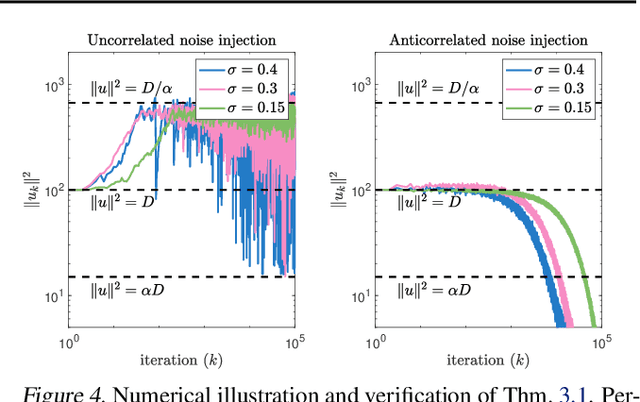
Injecting artificial noise into gradient descent (GD) is commonly employed to improve the performance of machine learning models. Usually, uncorrelated noise is used in such perturbed gradient descent (PGD) methods. It is, however, not known if this is optimal or whether other types of noise could provide better generalization performance. In this paper, we zoom in on the problem of correlating the perturbations of consecutive PGD steps. We consider a variety of objective functions for which we find that GD with anticorrelated perturbations ("Anti-PGD") generalizes significantly better than GD and standard (uncorrelated) PGD. To support these experimental findings, we also derive a theoretical analysis that demonstrates that Anti-PGD moves to wider minima, while GD and PGD remain stuck in suboptimal regions or even diverge. This new connection between anticorrelated noise and generalization opens the field to novel ways to exploit noise for training machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge