An Interior Point Method Solving Motion Planning Problems with Narrow Passages

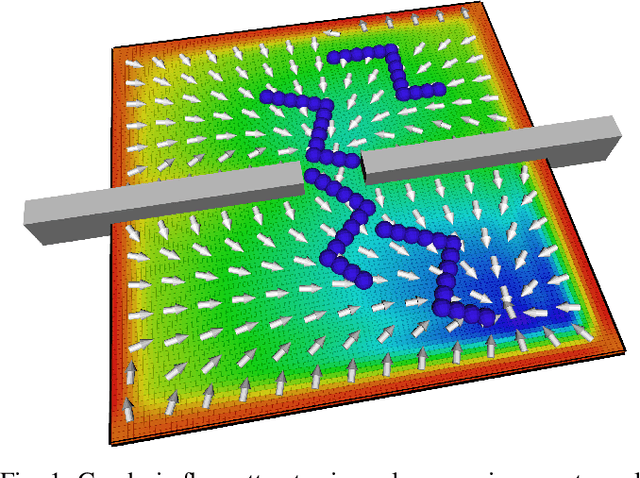
Algorithmic solutions for the motion planning problem have been investigated for five decades. Since the development of A* in 1969 many approaches have been investigated, traditionally classified as either grid decomposition, potential fields or sampling-based. In this work, we focus on using numerical optimization, which is understudied for solving motion planning problems. This lack of interest in the favor of sampling-based methods is largely due to the non-convexity introduced by narrow passages. We address this shortcoming by grounding the motion planning problem in differential geometry. We demonstrate through a series of experiments on 3 Dofs and 6 Dofs narrow passage problems, how modeling explicitly the underlying Riemannian manifold leads to an efficient interior-point non-linear programming solution.