An End-to-End Geometric Deficiency Elimination Algorithm for 3D Meshes

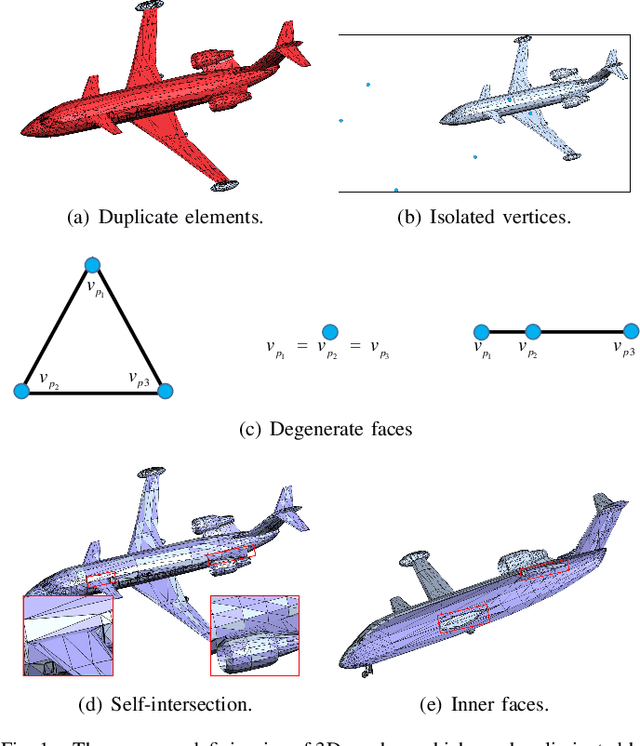
The 3D mesh is an important representation of geometric data. In the generation of mesh data, geometric deficiencies (e.g., duplicate elements, degenerate faces, isolated vertices, self-intersection, and inner faces) are unavoidable and may violate the topology structure of an object. In this paper, we propose an effective and efficient geometric deficiency elimination algorithm for 3D meshes. Specifically, duplicate elements can be eliminated by assessing the occurrence times of vertices or faces, degenerate faces can be removed according to the outer product of two edges; since isolated vertices do not appear in any face vertices, they can be deleted directly; self-intersecting faces are detected using an AABB tree and remeshed afterward; by simulating whether multiple random rays that shoot from a face can reach infinity, we can judge whether the surface is an inner face, then decide to delete it or not. Experiments on ModelNet40 dataset illustrate that our method can eliminate the deficiencies of the 3D mesh thoroughly.