An Alternative to Variance: Gini Deviation for Risk-averse Policy Gradient
Paper and Code
Aug 09, 2023


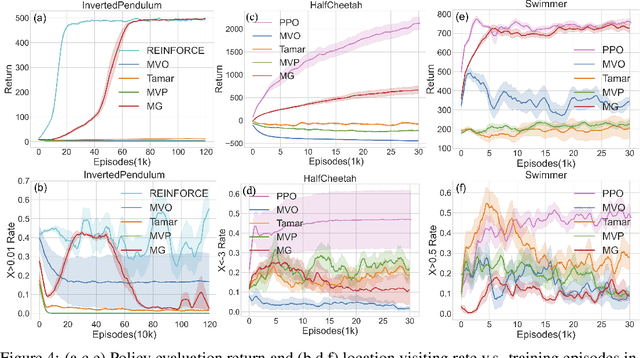
Restricting the variance of a policy's return is a popular choice in risk-averse Reinforcement Learning (RL) due to its clear mathematical definition and easy interpretability. Traditional methods directly restrict the total return variance. Recent methods restrict the per-step reward variance as a proxy. We thoroughly examine the limitations of these variance-based methods, such as sensitivity to numerical scale and hindering of policy learning, and propose to use an alternative risk measure, Gini deviation, as a substitute. We study various properties of this new risk measure and derive a policy gradient algorithm to minimize it. Empirical evaluation in domains where risk-aversion can be clearly defined, shows that our algorithm can mitigate the limitations of variance-based risk measures and achieves high return with low risk in terms of variance and Gini deviation when others fail to learn a reasonable policy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge