AdaWISH: Faster Discrete Integration via Adaptive Quantiles
Paper and Code
Oct 13, 2019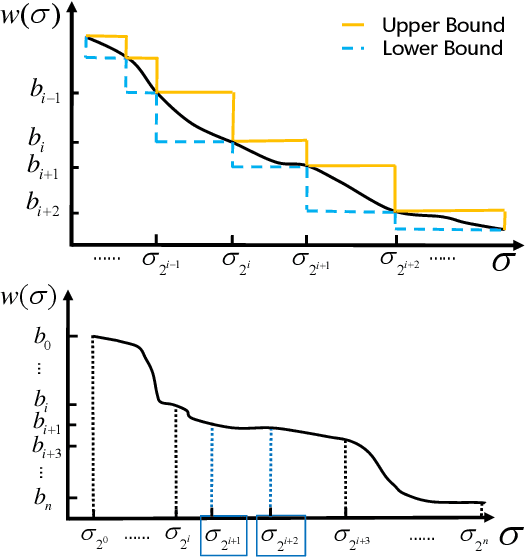
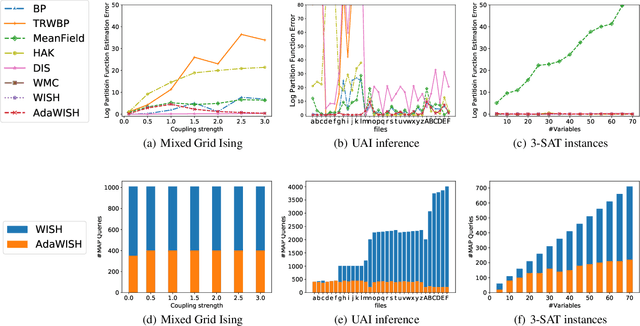
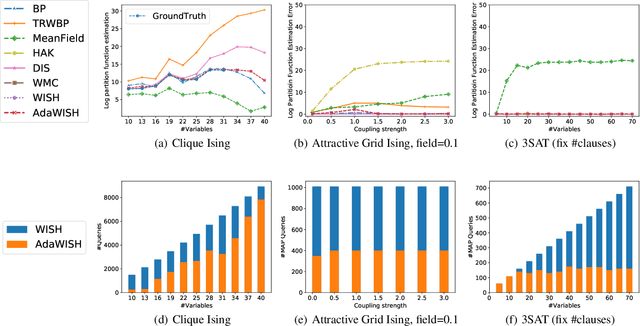
Discrete integration in a high dimensional space of $n$ variables poses fundamental challenges. The WISH algorithm reduces the intractable discrete integration problem into $n$ optimization queries subject to randomized constraints, obtaining a constant approximation guarantee. The optimization queries are expensive, which limits the applicability of WISH. We propose AdaWISH, which is able to obtain the same guarantee, but accesses only a small subset of queries of WISH. For example, when the number of function values is bounded by a constant, AdaWISH issues only $O(\log n)$ queries. The key idea is to query adaptively, taking advantage of the shape of the weight function. In general, we prove that AdaWISH has a regret of no more than $O(\log n)$ relative to an oracle that issues queries at data-dependent optimal points. Experimentally, AdaWISH gives precise estimates for discrete integration problems, of the same quality as that of WISH and better than several competing approaches, on a variety of probabilistic inference benchmarks, while saving substantially on the number of optimization queries compared to WISH. For example, it saves $81.5\%$ of WISH queries while retaining the quality of results on a suite of UAI inference challenge benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge