Adaptive Stochastic Natural Gradient Method for One-Shot Neural Architecture Search
Paper and Code
May 21, 2019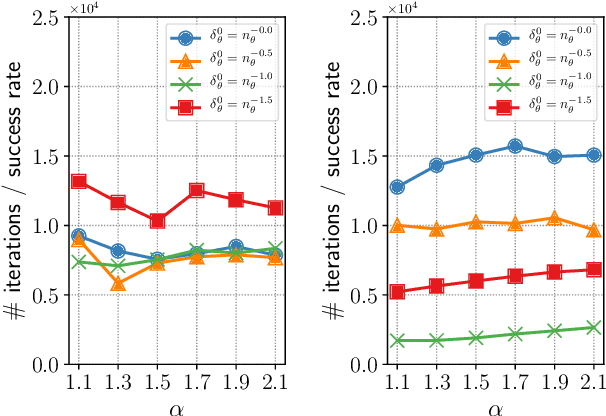
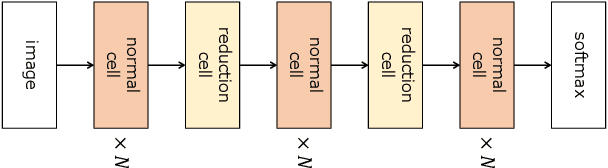
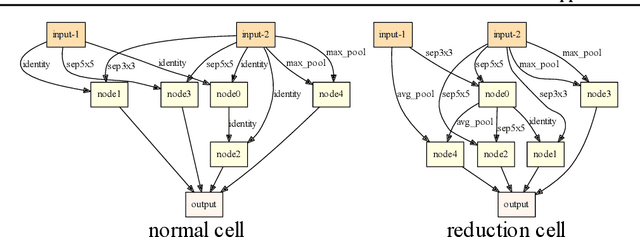
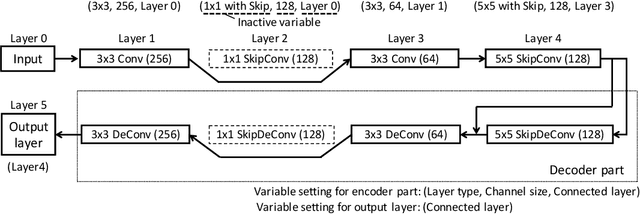
High sensitivity of neural architecture search (NAS) methods against their input such as step-size (i.e., learning rate) and search space prevents practitioners from applying them out-of-the-box to their own problems, albeit its purpose is to automate a part of tuning process. Aiming at a fast, robust, and widely-applicable NAS, we develop a generic optimization framework for NAS. We turn a coupled optimization of connection weights and neural architecture into a differentiable optimization by means of stochastic relaxation. It accepts arbitrary search space (widely-applicable) and enables to employ a gradient-based simultaneous optimization of weights and architecture (fast). We propose a stochastic natural gradient method with an adaptive step-size mechanism built upon our theoretical investigation (robust). Despite its simplicity and no problem-dependent parameter tuning, our method exhibited near state-of-the-art performances with low computational budgets both on image classification and inpainting tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge