Adaptive Stochastic ADMM for Decentralized Reinforcement Learning in Edge Industrial IoT

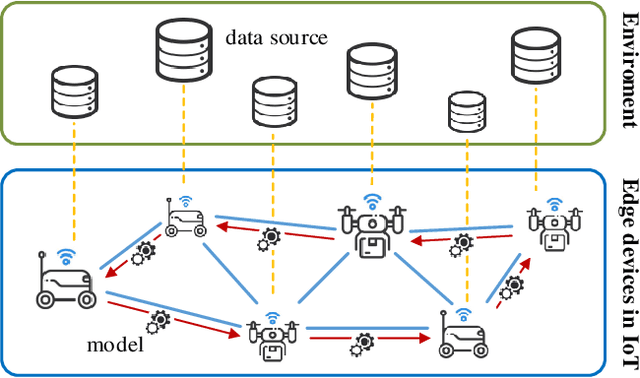
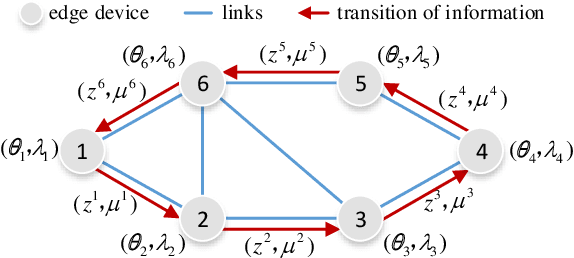
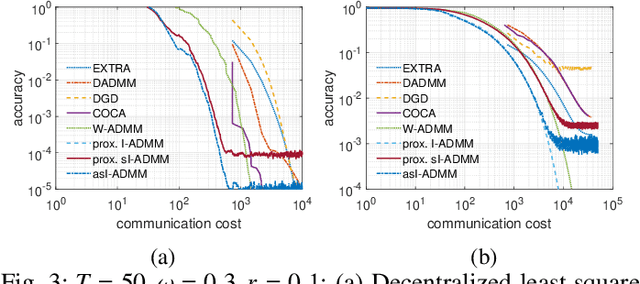
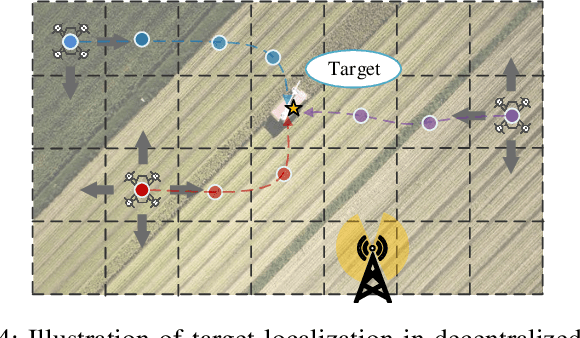
Edge computing provides a promising paradigm to support the implementation of Industrial Internet of Things (IIoT) by offloading tasks to nearby edge nodes. Meanwhile, the increasing network size makes it impractical for centralized data processing due to limited bandwidth, and consequently a decentralized learning scheme is preferable. Reinforcement learning (RL) has been widely investigated and shown to be a promising solution for decision-making and optimal control processes. For RL in a decentralized setup, edge nodes (agents) connected through a communication network aim to work collaboratively to find a policy to optimize the global reward as the sum of local rewards. However, communication costs, scalability and adaptation in complex environments with heterogeneous agents may significantly limit the performance of decentralized RL. Alternating direction method of multipliers (ADMM) has a structure that allows for decentralized implementation, and has shown faster convergence than gradient descent based methods. Therefore, we propose an adaptive stochastic incremental ADMM (asI-ADMM) algorithm and apply the asI-ADMM to decentralized RL with edge-computing-empowered IIoT networks. We provide convergence properties for proposed algorithms by designing a Lyapunov function and prove that the asI-ADMM has $O(\frac{1}{k}) +O(\frac{1}{M})$ convergence rate where $k$ and $ M$ are the number of iterations and batch samples, respectively. Then, we test our algorithm with two supervised learning problems. For performance evaluation, we simulate two applications in decentralized RL settings with homogeneous and heterogeneous agents. The experiment results show that our proposed algorithms outperform the state of the art in terms of communication costs and scalability, and can well adapt to complex IoT environments.