Adaptive Pruning of Pretrained Transformer via Differential Inclusions
Paper and Code
Jan 06, 2025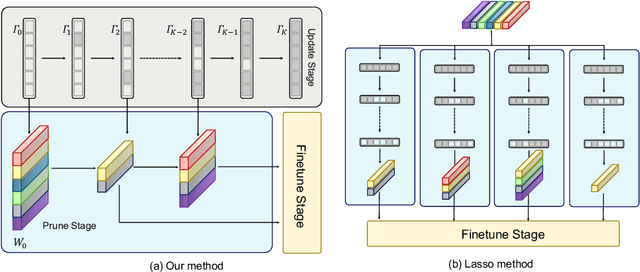
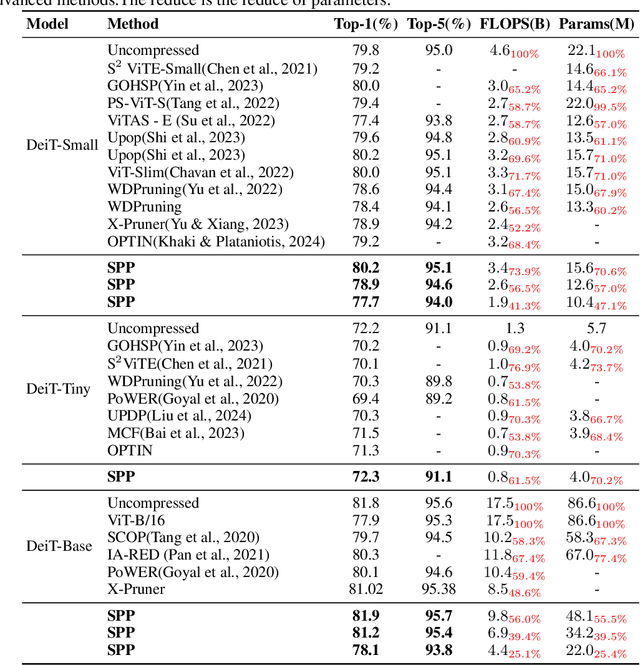
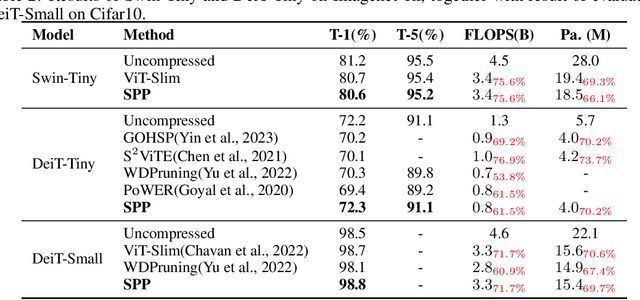
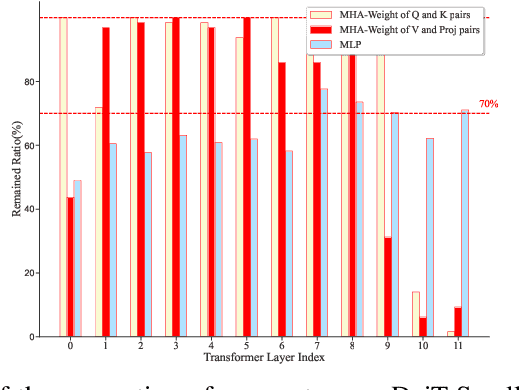
Large transformers have demonstrated remarkable success, making it necessary to compress these models to reduce inference costs while preserving their perfor-mance. Current compression algorithms prune transformers at fixed compression ratios, requiring a unique pruning process for each ratio, which results in high computational costs. In contrast, we propose pruning of pretrained transformers at any desired ratio within a single pruning stage, based on a differential inclusion for a mask parameter. This dynamic can generate the whole regularization solution path of the mask parameter, whose support set identifies the network structure. Therefore, the solution path identifies a Transformer weight family with various sparsity levels, offering greater flexibility and customization. In this paper, we introduce such an effective pruning method, termed SPP (Solution Path Pruning). To achieve effective pruning, we segment the transformers into paired modules, including query-key pairs, value-projection pairs, and sequential linear layers, and apply low-rank compression to these pairs, maintaining the output structure while enabling structural compression within the inner states. Extensive experiments conducted on various well-known transformer backbones have demonstrated the efficacy of SPP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge