Adaptive Least Mean Squares Estimation of Graph Signals
Paper and Code
Jul 11, 2016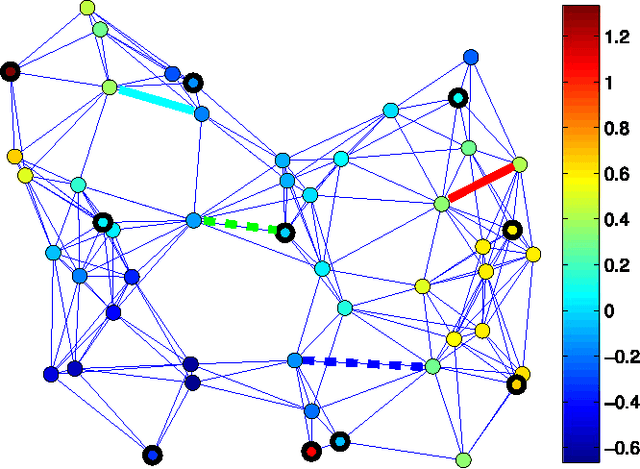
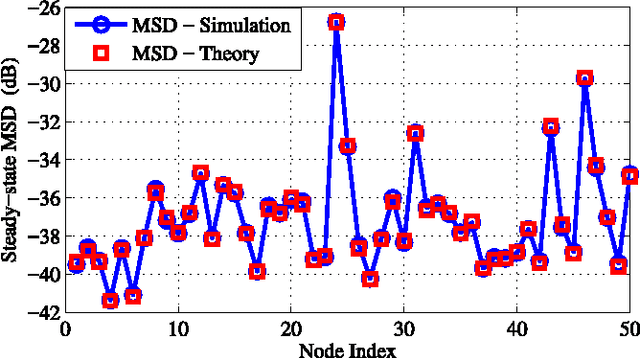
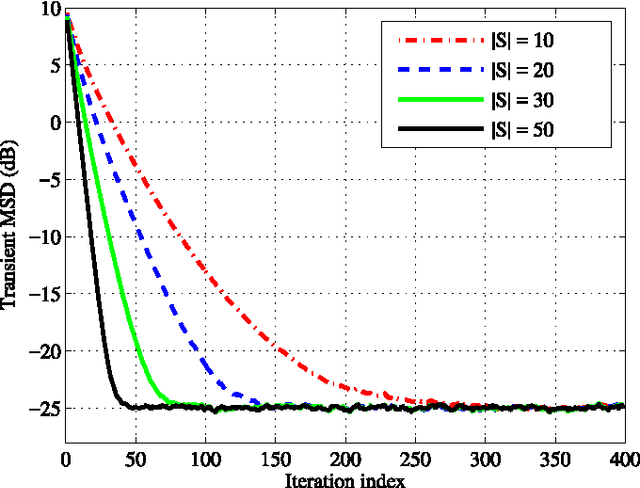

The aim of this paper is to propose a least mean squares (LMS) strategy for adaptive estimation of signals defined over graphs. Assuming the graph signal to be band-limited, over a known bandwidth, the method enables reconstruction, with guaranteed performance in terms of mean-square error, and tracking from a limited number of observations over a subset of vertices. A detailed mean square analysis provides the performance of the proposed method, and leads to several insights for designing useful sampling strategies for graph signals. Numerical results validate our theoretical findings, and illustrate the performance of the proposed method. Furthermore, to cope with the case where the bandwidth is not known beforehand, we propose a method that performs a sparse online estimation of the signal support in the (graph) frequency domain, which enables online adaptation of the graph sampling strategy. Finally, we apply the proposed method to build the power spatial density cartography of a given operational region in a cognitive network environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge