Accuracy to Throughput Trade-offs for Reduced Precision Neural Networks on Reconfigurable Logic

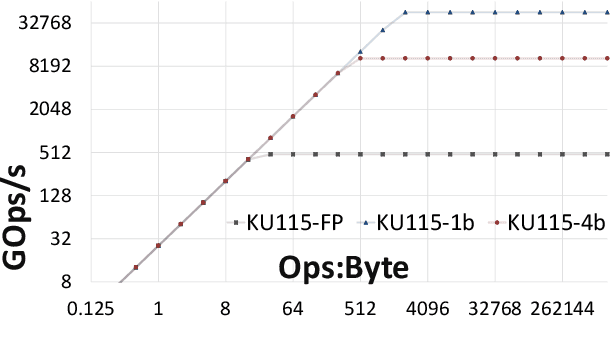
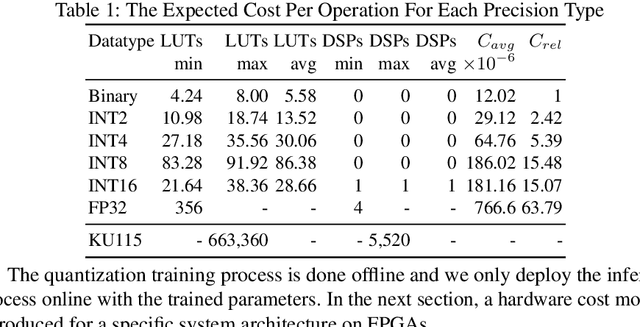
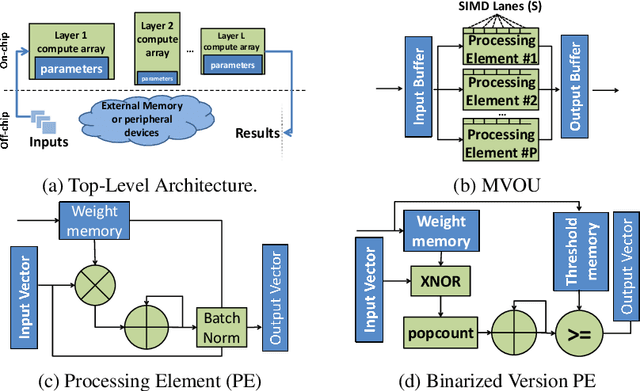
Modern CNN are typically based on floating point linear algebra based implementations. Recently, reduced precision NN have been gaining popularity as they require significantly less memory and computational resources compared to floating point. This is particularly important in power constrained compute environments. However, in many cases a reduction in precision comes at a small cost to the accuracy of the resultant network. In this work, we investigate the accuracy-throughput trade-off for various parameter precision applied to different types of NN models. We firstly propose a quantization training strategy that allows reduced precision NN inference with a lower memory footprint and competitive model accuracy. Then, we quantitatively formulate the relationship between data representation and hardware efficiency. Our experiments finally provide insightful observation. For example, one of our tests show 32-bit floating point is more hardware efficient than 1-bit parameters to achieve 99% MNIST accuracy. In general, 2-bit and 4-bit fixed point parameters show better hardware trade-off on small-scale datasets like MNIST and CIFAR-10 while 4-bit provide the best trade-off in large-scale tasks like AlexNet on ImageNet dataset within our tested problem domain.